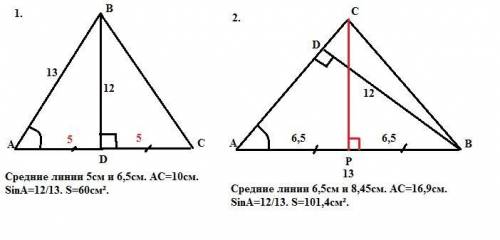
1. Средние линии 5см и 6,5см. АС=10см. SinA=12/13. S=60см².
2. Средние линии 6,5см и 8,45см. АС=16,9см. SinA=12/13. S=101,4см².
Объяснение:
Так как в условии явно не указано, какая из сторон является основанием, необходимо рассмотреть два варианта.
1. Если основание равнобедренного треугольника АС, боковые стороны АВ = ВС = 13см, а высота BD=12см к основанию АС, то AD=DC и по Пифагору АD = √(АВ²-BD²) = √(13²-12²) = 5см. =>
АС = 10см.
Средние линии треугольника АВС равны 5см (средняя линия, параллельная основанию) и 6,5см (средняя линия, параллельная боковой стороне).
SinA = BD/AB = 12/13.
Sabc = (1/2)*10*12 = 60см² или
Sabc = (1/2)*AB*AC*SinA = (1/2)*13*10*(12/13) = 60 см².
2. Если основание равнобедренного треугольника АВ=13см, боковые стороны АС = СВ, а высота BD=12см к боковой стороне АС, то
SinA = BD/AB = 12/13 (из прямоугольного треугольника ABD). =>
CosA = √(1 - Sin²A) = 5/13.
Проведем высоту СР к основанию АВ. Тогда АР=РВ = АВ/2 =6,5 см.
Из прямоугольного треугольнока АСР найдем АС:
АС = АР/CosA = 6,5*13/5 = 16,9см.
Sabc =(1/2)BD*AC = 101,4 см². Или
Sabc = (1/2)*AB*AC*SinA = (1/2)*13*16,9*(12/13) = 101,4 см².
Cредние линии треугольника АВС равны 6,5см (средняя линия, параллельная основанию) и 8,45см (средняя линия, параллельная боковой стороне).
Рассмотрим образованную пирамиду АВСК. КВ перпендикулярно АВС, значит нам необходимо найти длину высоты, опущенной в грани АСК из вершины К на АС. По теореме о трех перпендикулярах ее проекция на плоскость АВС будет перпендикулярна АС. Обозначим точку пересечения высоты с АС через Н. Тогда нужно найти КН.
Рассмотрим основание пирамиды - треугольник АВС. Он равнобедренный АС=ВС=10, с углом у основания А=30 градусов. Опустим высоту из вершины треугольника С на АВ - СМ. Высота, опущенная из точки С, будет и биссектрисой, и медианой треугольника. То есть АМ=МВ. Треугольник АСМ - прямоугольный, с одним из осмтрых углов = 30 градусов, значит катет, лежащий против этого угла, равен половине гипотенузы: АМ=1/2*АС, АМ=1/2*10=5 (см). По теореме Пифагора найдем второй катет СМ:
CM=sqrt(AC2-AM2)
CM=sqrt(100-25)=sqrt75=5sqrt3
BH- проекция КН на плоскость основания АВС, и, как было уже отмечено, ВН перпендикулярна АС. Рассм отрим треугольники АНВ и АМС- они подобны:
АН/АМ=НВ/МС=АВ/АС
НВ/МС=АВ/АС
НВ=МС*АВ/АС
НВ=5*(2*5sqrt3)/10=5sqrt3
Треугольник КНВ - прямоугольный (КВ перпендикулярно плоскости АВС). По теореме Пифагора найдем КН:
KH2=KB2+HB2
KH=sqrt(25+75)=sqrt100=10 (см)