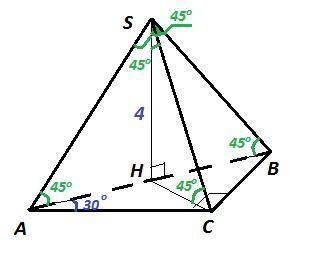
Дано: пирамида SABC, SH⊥(ABC), SH = 4 см,
∠ASH=∠CSH=∠BSH=45°, ∠ACB=90°, ∠BAC=30°
Найти : Sбок
Решение : так как боковые рёбра образуют с высотой пирамиды равные углы, значит, они образуют равные углы с основанием пирамиды (острые углы прямоугольных треугольников, равных по общему катету и острому углу). ⇒ Высота опускается в центр окружности, описанной около основания пирамиды. Основание пирамиды - прямоугольный треугольник, центр описанной окружности лежит на середине гипотенузы. H ∈ AB, AH = BH.
SH⊥(ABC) ⇒ SH⊥AB ⇒ ∠SHA=90°
ΔSAH - прямоугольный равнобедренный, так как ∠SAH=∠ASH=45° ⇒ AH = SH = 4 см ⇒ AB = AH + BH = 8 см; SA = 4√2 см
SA = SB = SC = 4√2 см
ΔABC - прямоугольный. Катет, лежащий против угла 30°, равен половине гипотенузы. BC = AB/2 = 4 см
По теореме Пифагора
AC² = AB² - BC² = 8² - 4² = 48
AC = √48 = 4√3 см
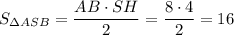 см²
см²
Площадь двух других граней можно найти по формуле Герона
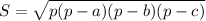
ΔASC, 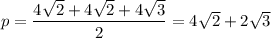
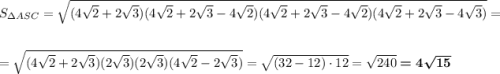
ΔBSC, 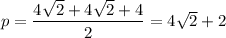
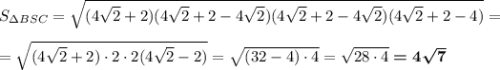
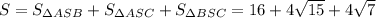
ответ: 4(4 + √15 + √7) см²
Дано: пирамида SABC, SH⊥(ABC), SH = 4 см,
∠ASH=∠CSH=∠BSH=45°, ∠ACB=90°, ∠BAC=30°
Найти : Sбок
Решение : так как боковые рёбра образуют с высотой пирамиды равные углы, значит, они образуют равные углы с основанием пирамиды (острые углы прямоугольных треугольников, равных по общему катету и острому углу). ⇒ Высота опускается в центр окружности, описанной около основания пирамиды. Основание пирамиды - прямоугольный треугольник, центр описанной окружности лежит на середине гипотенузы. H ∈ AB, AH = BH.
SH⊥(ABC) ⇒ SH⊥AB ⇒ ∠SHA=90°
ΔSAH - прямоугольный равнобедренный, так как ∠SAH=∠ASH=45° ⇒ AH = SH = 4 см ⇒ AB = AH + BH = 8 см; SA = 4√2 см
SA = SB = SC = 4√2 см
ΔABC - прямоугольный. Катет, лежащий против угла 30°, равен половине гипотенузы. BC = AB/2 = 4 см
По теореме Пифагора
AC² = AB² - BC² = 8² - 4² = 48
AC = √48 = 4√3 см
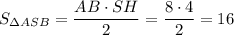 см²
см²
Площадь двух других граней можно найти по формуле Герона
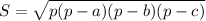
ΔASC, 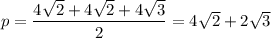
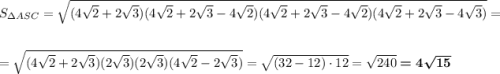
ΔBSC, 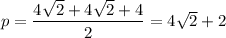
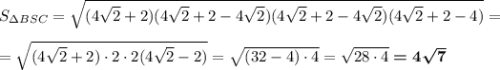
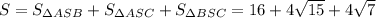
ответ: 4(4 + √15 + √7) см²

В решении задачи пригодится
1)Теорема о трех перпендикулярах.
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна этой наклонной.
2) Теорема Пифагора.
Решение.
Основание АВСD пирамиды SАBСD- прямоугольник.
Наклонные SB и SD имеют проекции ВС и CD
Прямая ВА перпендикулярна проекции ВС наклонной SB.
АВ перпендкулярна SB.
Прямая АD перпендикулярна проекции СD наклонной SD.
АD перпендикулярна SD
Углы SDА и SВА - прямые.
Следовательно, Δ SDА и ΔSВА - прямоугольные.
SС перпендикулярна плоскости основания, ⇒ перпендикулярна ВС и СD.
Δ SСB и ΔSСD - прямоугольные.
Все грани пирамиды пирамиды SАBСD - прямоугольные треугольники.
Площадь прямоугольного треугольника равна половине произведения его катетов.
Катеты треугольников SСB и SСD даны в условии задачи.
Это SС и СB в треугольнике SСB,
Это SС и СD в треугольнике SСD.
Катеты треугольника SВА - сторона ВС основания и
гипотенуза SВ треугольника SСB
Катеты треугольника SDА - сторона СD основания и
гипотенуза SD треугольника SСD.
Найдем SВ и SD по теореме Пифагора.
SD =√(СD² +SС²)=√(9²+12²)=15 см
SВ =√(SС²+ВС²)=√(16²+12²)=20 см
Площадь боковой поверхности пирамиды равна сумме площадей боковых граней пирамиды.
Площадь Δ SCВ =СS·BC:2=12·16:2
-"-"-"-"-"-"- Δ SВА=SВ·ВА:2=20·9:2
-"-"-"-"-"-"- Δ SDА=SD·DА:2=15·16:2
-"-"-"-"-"-"- Δ SСD=SC·СD:2=12·9:2
S боковая=(12·16+20·9+15·16+12·9):2
S боковая=(192+ 180+ 240+108):2=360 см²