пусть ad> bc , тогда острые углы равные 75 и 15 гр лежат при оснований ad , положим что y,w середины сторон ab и cd соответственно , тогда yw средняя линия трапеции , значит ad+bc=2yw из условия мы знаем что yw равна либо 15 либо 7 , положим что ab и cd пересекаются в точке e , тогда aed=180-(75+15)=90 , положим также что z,x это середины сторон основании bc,ad соотвественно , пусть n точка пересечения yw и zx , тогда по замечательному свойству трапеции точки e,z,x лежат на одной прямой , учитывая что угол aed прямой , получаем что ax=ex=ad/2 , ez=bz=bc/2 , но так как ex=ez+zx откуда окончательно получаем две системы
{ad-bc=2*7
{ad+bc=2*15
или
{ad-bc=2*15
{ad+bc=2*7
подходит решение первой системы , так как они положительны , складывая получаем ad=22 , bc=8 , значит ответ bc=8.
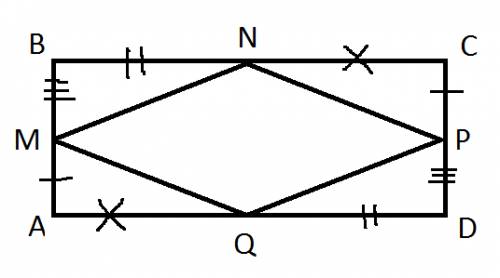
BC=BN+NC; AD=AQ+QD, т.к. BN=DQ, а NC=QA, то BC=AD.
Аналогично BA=CD.
ABCD- параллелограмм, т.к. AB=CD, BC=AD ( если противоположные стороны в 4-угольнике попарно равны, то этот 4-угольник - параллелограмм).
Рассмотрим ▲MBN и ▲PDQ.
1) BN=DQ - по условию.
2) BM=DP - по условию.
3) ∠B =∠D, т.к. они противоположные углы в параллелограмме равны.
▲MBN =▲PDQ по 2 сторонам и углу между ними.
Значит MN=QP, как соответствующие элементы в равных треугольниках.
Рассмотрим ▲NCP и ▲MAQ.
1) АМ=СР - по условию.
2) NC=QA - по условию.
3) ∠A= ∠C, т.к. они противоположные углы в параллелограмме.
▲NCP =▲MAQ по 2 сторонам и углу между ними.
Значит NP=MQ, как соответствующие элементы в равных треугольниках.
MN=QP,NP=MQ , значит MNPQ - параллелограмм ( если противоположные стороны в 4-угольнике попарно равны, то этот 4-угольник - параллелограмм).
Чертеж получился корявенький, но думаю суть ты уловил. Только рисуй именно параллелограмм, а не прямоугольник, учителя обычно к этому жутко придераются, а у меня в Paint был только прямоугольник.
Вершины ΔАВС находятся в точка А(1,0,2) В(3,3,3) С(2,1,0) найти: а)внешний угол при вершине В , б)длины сторон треугольника.
Объяснение:
а)Пусть внешний угол при вершине В будет β. Тогда β=180°-∠АВС , по т. о смежных углах.
BA*ВC=|BA|*|BC|cos(∠АВС) .
Координаты векторов ВА(-2;3;-1) , ВC(-1;-2;-3), длины векторов
|BA|=АВ=√( (-2)²+3²+(-1)²)=√14,
|BC|=√( (-1)²+(-2)²+(-3)²)=√14,
2-6+3=√14*√14*cos(∠АВС), cos(∠АВС)=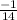 ,
,
∠АВС=arccos(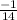 )=π-arccos(
)=π-arccos(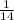 )
)
Тогда β=180-(π-arccos(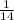 ) )=arccos(
) )=arccos(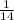 )
)
б)АВ=√( (3-1)²+(3-0)²+(3-2)²)=√14,
ВС=√( (2-3)²+(1-3)²+(0-3)²)=√14,
АС=√( (2-1)²+(1-0)²+(0-2)² )=√6.