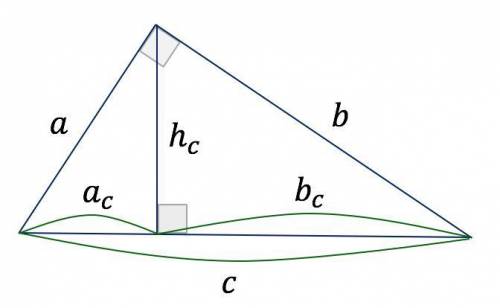
Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою  і проекцією цього катета на гіпотенузу:
і проекцією цього катета на гіпотенузу:
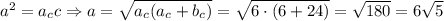 см
см
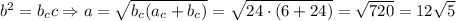 см
см
Площа 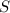 прямокутного трикутника знаходится як півдобуток його катетів:
прямокутного трикутника знаходится як півдобуток його катетів:
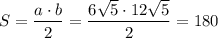 см²
см²
Другий б
Висота 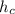 прямокутного трикутника, що проведена до гіпотенузи
прямокутного трикутника, що проведена до гіпотенузи  з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
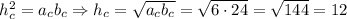 см
см
Площа 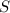 будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи
будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи  і висоти
і висоти 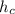 , що до неї проведена:
, що до неї проведена:
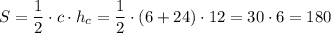 см²
см²
Відповідь: 180 см².
2пr = 8п
2r=8п:п
2r =8
r=4-рдиус вписан. окр.
S впис. окр = пr2
S=3,14*4*4= 50,24 - плозадь впис окр.
Плозадь окр, опис. вокруг правильного треуг. в 4 раза больше
S опис. окр. =50,24*4=200,96
S кольца = S опис. окр.- S впис. окр.
S кольца= 200,96- 50,24= 150,72
В треуг ABCD проведем медеаны,AD,BK,CM.
S треуг. ABCD 1/2 AC*BK, 1/2 AC=KC
Медиана треуг. впис окр. делится в отношении 2:1
Поэтому высота BK=R+r=8+4=12
S=12*KC
Найдем KC - сторону треуг. KOC, KC-касат.,OC=R=8-гипотинуза, другой катет ОK=r=4
KC2=OC2+OK2
KC-корень из 8*8-4*4= корень из 48= 6,92
Sтреуг. ABC=12*6,92=83,04
Прости,но без рисунка.