а) сс1; б) а1с; в) bc1 = d1c1 - d1b.
Объяснение:
Правила:
СУММА. Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную).
РАЗНОСТЬ. Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Тогда:
Вектор ca1+ad+d1c1 = ca1+a1d1+d1c1 = сс1 (вектор ad = вектору а1d1)
Вектор ab-aa1-c1b1 = a1b-c1b1 = d1c-d1a1 = a1c (вектор a1b = вектору d1c).
Вектор bc1 = d1с1 - d1b

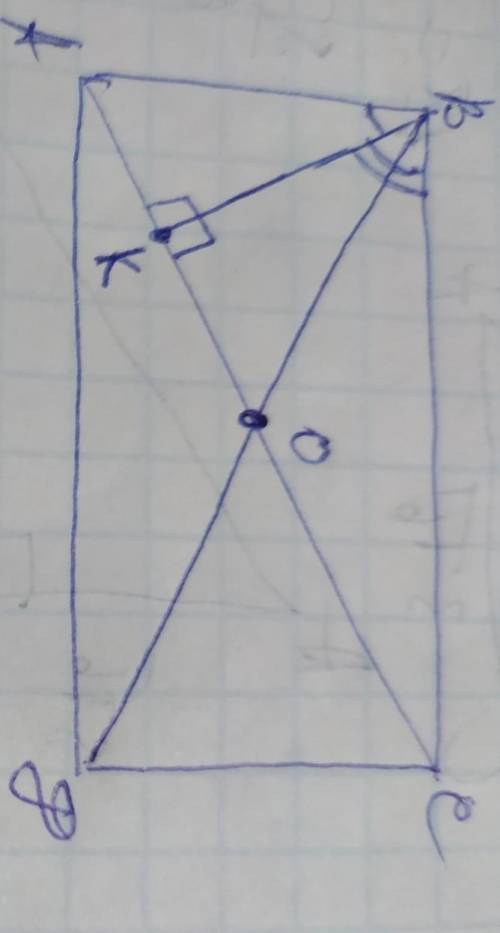
угол КВО=45°
Объяснение:
обозначим вершины прямоугольника ABCD с диагоналями АС и ВД, точку их пересечения О, а перпендикуляр ВК, пропорции углов обозначим х и 3х и, так как сумма этих двух углов составляет 90°, составим уравнение:
х+3х=90
4х=90
х=90÷4
х=22,5.
Итак: угол АВК=22,5°, тогда угол КВС=22,5×3=67,5°.
Рассмотрим полученный ∆АВК. Он прямоугольный, угол АВК=22,5°, а так как сумма острых углов прямоугольного треугольника составляет 90°, то угол ВАК=90-22,5=67,5°.
Рассмотрим ∆АВО. Он равнобедренный, поскольку диагонали прямоугольника пересекаясь делятся пополам, поэтому АО=ВО, а АВ- его основание и углы при основании равны:
уголВАО=углу АВО=67,5°. Угол ВАО в ∆АВО и угол ВАК в ∆АВК является общим и равен 67,5°. Тогда угол КВО=67,5-22,5=45°
Задача имеет два случая, т.к. диагональю АС может быть и большая и меньшая диагональ параллелограмма.
1 случай. Пусть АС- меньшая диагональ, тогда по теореме cos-ов
AC^2=a^2+b^2-2*a*b*cos30=16+48-48=16, тогда АС=4.
Из прямоугольного треугольника АС1С, H=AC*tg60=4*корень(3).
S(бок)=P*H=2*(4+4*корень(3))*4*корень(3).
2 случай. АС - большая диагональ: AC^2=a^2+b^2-2/a*b*cos150=16+48+48=112,
AC=4*корень(7). Тогда H=4*корень(21).S(бок)=P*H=2*(4+4*корень(3))*4*корень(21).