
Из треугольника АВС по теореме косинусов:
ВС² = AB² + AC² - 2·AB·AC·cosA = 25 + 16 - 2 · 5 · 4 · 1/2
BC² = 41 - 20 = 21
BC = √21 см
Плоскости АВС и α параллельны, АВ лежит в плоскости АВС, значит АВ║α.
Параллельные прямые АА₁ и ВВ₁ задают плоскость. Назовем ее β.
Через прямую АВ, параллельную плоскости α, проходит плоскость β и пересекает плоскость α. Тогда линия пересечения плоскостей параллельна прямой АВ.
Итак, АВ║А₁В₁, АА₁║ВВ₁, значит АА₁В₁В - параллелограмм, значит АВ = А₁В₁.
Аналогично доказываем, что ВС = В₁С₁ и АС = А₁С₁.
Тогда ΔА₁В₁С₁ равен ΔАВС по трем сторонам. Значит
А₁В₁ = АВ = 5 см,
В₁С₁ = ВС = √21 см
А₁С₁ = АС = 4 см.
1) Отразим рисунок относительно прямой AB, окружности перейдут сами в себя, а K – перейдёт в точку K', симметричную относительно прямой AB. Если K не лежит на AB, то K и K' не совпадают, и K' – тоже точка касания, чего быть не может.
2) Радиусы, проведённые в точку касания, перпендикулярны касательной, поэтому AN и BM перпендикулярны NM, а тогда параллельны, ANMB – прямоугольная трапеция.
Проведём высоту трапеции AD. ANMD – прямоугольник, поэтому MD = AN = r, тогда BD = 2r. Кроме того, AB = AK + KB = 4r, поэтому ∠DAB = 30° (противолежащий катет равен половине гипотенузы), а по теореме Пифагора .
.
Площадь трапеции ANMB равна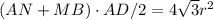
Площадь сектора KAN с центральным углом 90° + 30° = 120° = π/3 равна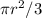
Площадь сектора KBM с центральным углом 90° - 30° = 60° = π/6 равна
Площадь искомой фигуры