ответ:
основание пирамиды – равнобедренный прямоугольный треугольник авс, угол с=90°, ас=вс=6 см. высота пирамиды - третье из смежных попарно перпендикулярных ребер=8 см.
площадь полной поверхности – сумма площади основания и площадей боковых граней.
s осн=ас•bc: 2=18 см²
грани амс=вмс по равенству катетов.
s ∆ amc=s ∆ bmc=6•8: 2=24
s amb=mh•ab: 2
ab=ac: sin45°=6√2
ch высота и медиана ∆ асв, сн=ав: 2=3√2
высота mh большей боковой грани s=√(ch*+mh*)=√(18+64)=√82
s∆amb=6√2•√82=6√164=12√41
s полн=18+2•24+12√41=66+12√41
объяснение:
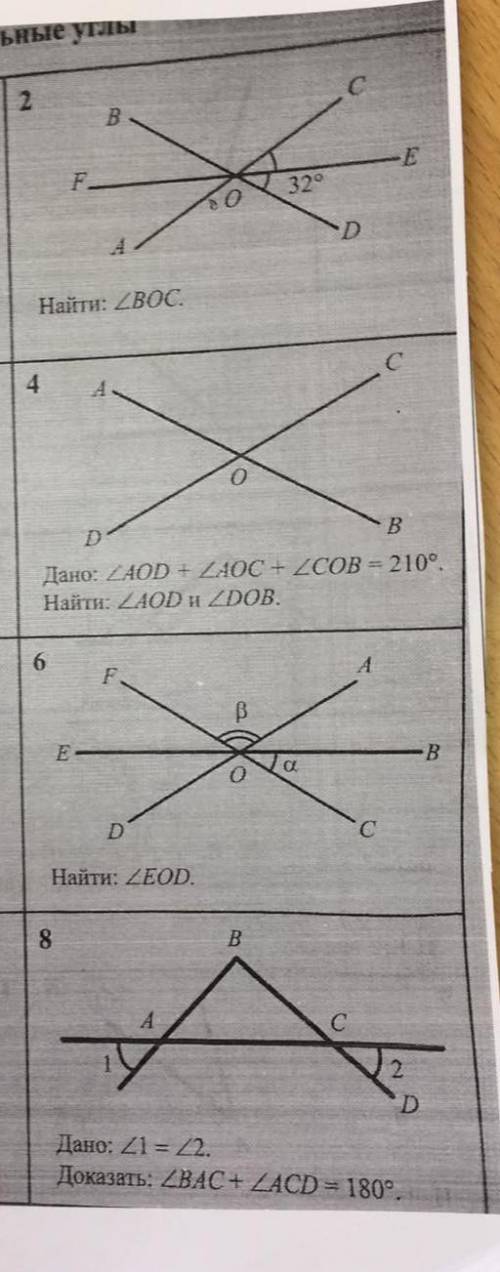
2. ∠BOC=116°
4. ∠AOD=30°, ∠DOB=150°
6. подумаю, дополню ответ
8. применима теорема смежных и вертикальных углов
Сумма смежных углов равна 180°
Объяснение:
2. ∠EOD=∠FOB=32°
180-32-32=116
4. ∠AOD+∠AOC=180°. так как к ним добавляется ∠COB и вместе 3 угла составляют 210° легко определить чему равен ∠COB
210-180=30°, ∠COB=30° он же равен углу ∠AOD , значит ∠AOD=30°,
таким образом находим ∠AOC, 180-30=150°, ∠AOC=∠DOB=150°
8. ∠1+∠А=180°
∠А+∠BAC=180°
∠C+∠BCA=180°
∠C+∠2=180°
∠C=∠ACD, ∠BAC=∠BCA, можно смело утверждать что ∠BAC+∠ACD=180°