Две прямые дороги KM и PN, которые пересекаются где-то за лесом в недоступной точке С. Нужно найти расстояние от некоторого пункта А на дороге КМ к точке С пересечения дорог. Для этого обозначили на дороге PN пункт В так, чтобы можно было измерить расстояние АВ, и определили углы ВАМ и ABN. Объясните нахождения расстояния АС. Вычислите АС, если АВ = 800 м , ∠ВАМ = 85°, ∠АВN = 52° .
Объяснение: Таким , зная определенные теоремы геометрии, можно не ходить часами с линейкой по дороге измеряя длину АС, а ВЫЧИСЛИТЬ ее по теореме синусов .
Теорема синусов :" Стороны треугольника пропорциональны синусам противолежащих углов."
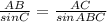. Видимый и измеряемый отрезок пути АВ=800 м. Угол ∠С вычисляется по т. о сумме углов треугольника, т.к два доступных угла можно измерить на местности с простейшей астролябии ( можно изготовить в домашних условиях) : ∠С=180°-85°-52°=43°.
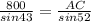, АС=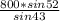 
≈ 
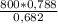≈ 924 (м).
Короче формула нахождения Площади равн. Тр.
a+b..
2. * h, где а и b основания , а h высота.
короче проведи сначала высоту из правого верхнего угла и потом напиши что катет лежащий против угла в 30 градусов равен одной второй гипотенузы , гипотенуза будет являться боковая правая сторона значит от т. Н до правого нижнего угла равно будет 5 см дальше по теореме Пифагора находишь больший катет, он же высота и уже подставляешь под формулу данные:)