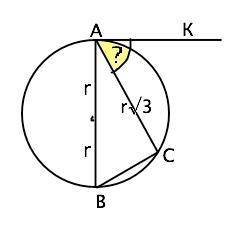
1) Пусть АВ – диаметр данной окружности, АС - хорда, АК - касательная.
В треугольнике АВС угол С=90° ( опирается на диаметр). АВ=2r, AC=r√3 ⇒ sin B=AC:AB ⇒ sin B=r√3:2r=√3/2.
Вписанный угол АВС равен половине дуги, на которую опирается. Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой (теорема) Следовательно, ∠КАС=∠АВС=arcsin √3/2 - это синус угла 60°.
* * *
2) Задача - обратная первой. Если угол КАС=60°, то вписанный угол АВС равен ему, т.е. ∠АВС=60°. Тогда хорда АС=АВ•sin60°=2r•√3/2=r√3
Сторона правильної чотирикутної піраміди дорівнює а , а її діагональний переріз – рівносторонній трикутник. Знайдіть об’єм піраміди. 2. Висота правильної чотирикутної піраміди дорівнює 12 см, а апофема – 15 см. Обчисліть площу бічної поверхні піраміди. 3. Сторона основи правильної трикутної піраміди дорівнює 6 см, а висота піраміди - см. Знайдіть площу бічної поверхні піраміди. 4. Сторона основи правильної трикутної піраміди дорівнює 8 см, а бічна грань нахилена до площини основи під кутом 300. Знайдіть площу повної поверхні піраміди. 5. Основа піраміди – трикутник зі сторонами 13 см, 14 см і 15 см. Знайдіть площу перерізу, який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:2. Рахуючи від вершини піраміди. Знайдіть об‘єм правильної чотирикутної піраміди, сторона основи якої дорівнює 6 см, а діагональний переріз є рівностороннім трикутником