Рассмотрим треугольник NPK.
Угол PKN = 90°, по условию задачи, значит треугольник NPK — прямоугольный. Угол PKN = 90°, угол KNP = 60°. Сумма углов треугольника равна 180°, значит угол NPK = 180° – 90° – 60° = 30°. Одно из свойств прямоугольного треугольника: катет, лежащий против угла в 30°, равен половине гипотенузы. Получается, KN = NP : 2. NP = 2 × KN = 2 × 5 см = 10 см. Воспользуемся теоремой Пифагора (квадрат гипотенузы равен сумме квадратов катетов) и найдем второй катет.
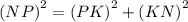
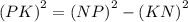
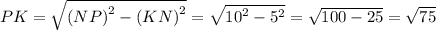см
Рассмотрим треугольник MPK. Идём по тому же пути.
Угол PKM = 90°, по условию задачи, значит треугольник MPK — тоже прямоугольный. Пользуемся тем же свойством прямоугольного треугольника: катет, лежащий против угла в 30°, равен половине гипотенузы. PK = MP : 2. MP = 2 × PK =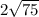 
см. Применяем теорему Пифагора и находим катет KM.
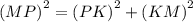
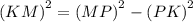
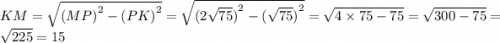см
Объяснение:
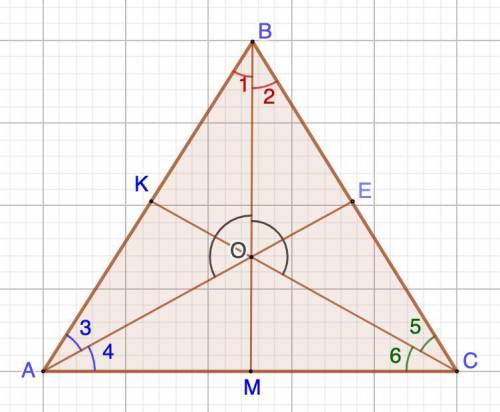
Дано: ΔАВС
АЕ, ВМ, СК - биссектрисы;
∠AOB = ∠ ВОС = 110°.
а) Доказать: ΔАВС - равнобедренный;
б) Найти: ∠А; ∠В; ∠С.
а) Доказательство:
Рассмотрим ΔАОВ и ΔВОС.
∠1=∠2 (условие)
∠AOB = ∠ ВОС (условие)
ВО - общая
⇒ ΔАОВ = ΔВОС (по 2 признаку)
⇒ АВ=ВС (как соответственные элементы)
⇒ ΔАВС - равнобедренный.
б) Решение:
1) ΔАОВ = ΔВОС ⇒АО=ОС (как соответственные элементы)
2) Рассмотрим ΔАОС (равнобедренный, п.1)
⇒ ∠4=∠6 (углы при основании равнобедренного треугольника равны)
∠АОС=360°-(∠AOB + ∠ ВОС)=360°-(110°+110°)=140°
Сумма углов треугольника равна 180°.
⇒ ∠4=∠6=(180°-140°):2=20°
3) ∠3=∠4 (условие)
⇒∠А=∠3+∠4=20°+20°=40°
4) ∠А=∠С=40° (при основании равнобедренного ΔАВС)
∠В=180°-(40°+40°)=100°
2,3,4наверрное так