Сделаем рисунок, хотя вполне можно обойтись без него.
Искомый угол - вписанный в окружность.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
В данном случае имеем два центральных угла:
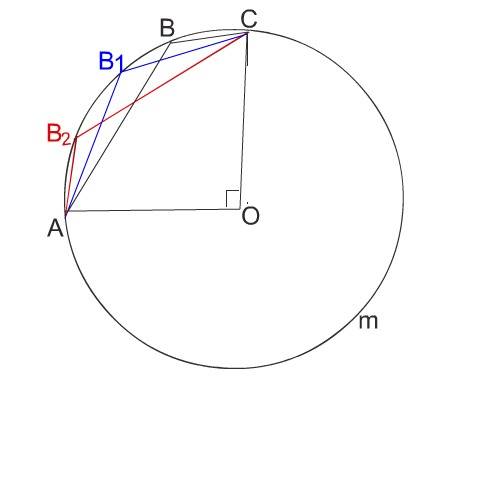
один находится внутри четырехугольника и равен 90°.
Второй - угол АОС (2) - вне его, опирается на дугу АmС и равен
360°- 90°=270°
Так как угол АВС четырехугольника опирается на ту же дугу в 270°, он равен половине центрального угла, опирающигося на ту же дугу и равен
270°:2=135°
Величина этого угла не зависит от того, в каком месте дуги АВС будет находиться вершина В четырехугольника АВСО.
Дано:
a=3
b=4
c=5
Найти:
угол между BC1 и A1BC
Решение:
Проведем в плоскости A1BC высоту из точки B в точку K(которая будет падать на A1C)
Докажем,что высота будет падать в середину A1C.
Т.к A1B=BC(доказывается через теорему пифагора),то трегольник A1BC-равнобедренный.
А значит высота падает в середину основания
Рассмотрим трегольник BKC1:
он прямогульный(угол K прямой)
Видим,что BK=C1K.
Т.к. диагонали равны и делятся пополам.
Значит угол между BC1 и A1BC равен тангенсу угла B из треугольника BKC1.
Т.к. tg=C1K/BK (а они равны)
Значит tg=1,т.е. угол равен 45 градусов.
ответ:45 градусов
По теореме Пифагора СА=13см 5в кв + 12 в кв = 169 корень 169=13
б) 5см