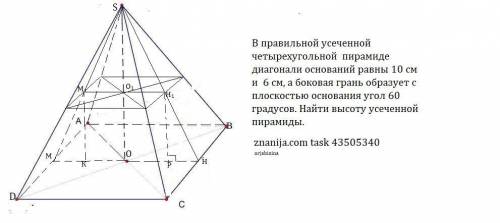
В правильной усеченной четырехугольной пирамиде диагонали оснований равны 10 см и 6 см, а боковая грань образует с плоскостью основания угол 60 градусов. Найти высоту усеченной пирамиды.
Объяснение:
1) АВСDA₁B₁C₁D₁- усеченная пирамида , Точки О и О₁ -точки пересечения диагоналей оснований Т.к пирамида правильная , то основания кавдраты.
АВСD- нижнее основание , по т. Пифагора АВ=√(10²:2)=5√2 (см).
A₁B₁C₁D₁-верхнее основание , по т. Пифагора A₁B₁=√(6²:2)=3√2 (см).
2) Проведем через точки О и О₁ отрезки МН и М₁Н₁ перпендикулярно сторонам квадратов.Тк О₁Н₁ ⊥ВС, то SH⊥ВС по т. о трех перпендикулярах . Поэтому линейным углом между плоскостью боковой грани и плоскостью основания будет ∠НН₁М=60°.
3) Рассмотрим сечение , проходящее через МН и М₁Н₁ перпендикулярно сторонам основаниям. В сечении получилась равнобедренная трапеция ММ₁Н₁Н.
Проведем высоты М₁К и Н₁Р в трапеции . Тогда КР=М₁Н₁ =3√2 см , а МК=РН=( 5√2-3√2):2=√2 (см).
ΔРНН₁ -прямоугольный , tg60°=PН₁ /PH , √3=PН₁ /√2 , PН₁ =√6 см.
Поэтому высота усеченной пирамиды √6 см.
10√3 см
Объяснение:
Длинная наклонная - с углом 30° с плоскостью
Высота равна половине длинной наклонной
h = l₁/2 = 15/2 см
Теорема Пифагора для второй наклонной l₂ как гипотенузы, высоты h как катета и проекции p₂ как катета против угла в 30°
l₂² = h² + p₂²
l₂² = h² + (l₂/2)²
l₂² = h² + l₂²/4
3/4*l₂² = h²
l₂ = 2h/√3
l₂ = 2*15/2/√3 = 5√3 см
Угол между наклонными 90°
Расстояние d между основаниями наклонных - гипотенуза, наклонные - катеты
l₁² + l₂² = d²
d² = 15² + (5√3)²
d² = 225 + 25*3 = 300
d = √300 = 10√3 см
ну, по свойству биссектрисы отрезки гипотенузы тоже относятся как 3/4. Пусть один из них 3*x, тогда 4*x, разность x = 5. Поэтому гипотенуза равна 7*5 = 35.
Катеты легко находятся из теоремы Пифагора при заданной пропорции, они равны 21 и 28. А площадь равна 294.
Задачу можно решить без каких-то "сложных" вычислений, если сразу увидеть, что отношение катетов 3/4 задает нам египетский треугольник, подобный (3,4,5). Сопоставляя эту тройку с длиной гипотенузы 35, видим, что длины сторон (21, 28, 35).