Question

Могут ли биссектрисы треугольника пересекаться под прямым углом?

Answer 1

I - точка пересечения биссектрис.

Треугольник AIB - прямоугольный, сумма острых углов 90.

IAB +IBA =A/2 +B/2 =90 => A+B =180,

что невозможно, так как угол С не может быть равен 0 (A+B+C=180).

Answer 2

Допустим, могут.

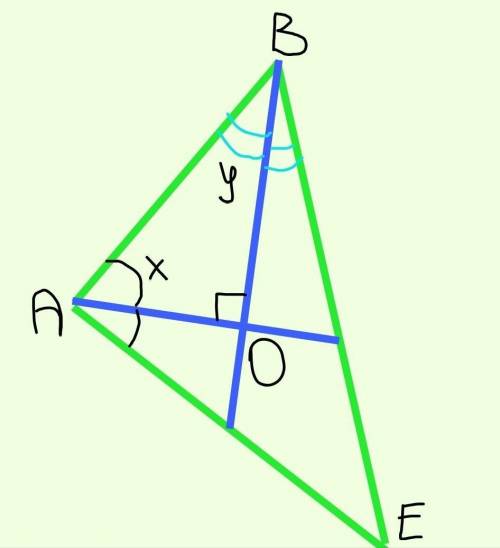
Тогда угол АОВ=90°.

Пусть угол ВАО=х, а угол АВО=у.

Сумма острых углов в прямоугольном треугольнике равна 90°. Тоесть угол ВАО+угол АВО=90°;

х+у=90

2(х+у)=90*2

2х+2у=180

Так как АО и ВО – биссектрисы углов ЕАВ и АВЕ соответственно, то угол ЕАО=угол ВАО=х; угол ОВЕ=угол АВО=у.

Из найденного: х+у=90 => 2х+2у=180

2х+2у=угол ЕАО+угол ВАО+угол ОВЕ+угол АВО

2х+2у=угол ЕАВ+угол АВЕ

=> Угол ЕАВ+угол АВЕ=180°

Сумма углов в любом треугольнике равна 180°.

Следовательно угол АЕВ=180°–(угол ЕАВ+угол АВЕ)=180°–180°=0°.

Величина угла выражается положительным числом, значит 0 она быть не может.

Получим что биссектрисы не могут пересекаться под прямым углом.

Получим что биссектрисы не могут пересекаться под прямым углом.ответ: Нет.