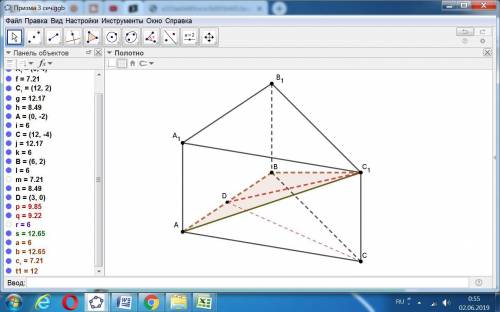
Обозначим сторону основания а, высоту призмы Н, высоту сечения h.
Проекция высоты сечения h на основание - это высота основания СD.
CD = a√3/2. Тогда высота призмы как катет, лежащий против угла 60 градусов, равна (a√3/2)*tg 60° = (a√3/2)*√3 = 3a/2.
Теперь определим высоту сечения h.
h = CD/cos 60° = (a√3/2)/(1/2) = a√3.
Площадь сечения как треугольника равна:
S(AC1B) = (1/2)a*h = (1/2)a*(a√3) = a²√3/2.
Приравняем заданному значению: a²√3/2 = 8√3, a² = 16, a = 4.
Можно получить ответ:
V = SoH = (a²√3/4)*(3a/2) = 3a³√3/8 = 3*64*√3/8 = 24√3 см³.
Параллельно боковой стороне CD трапеции ABCD проведена прямая BK
основания трапеции тоже параллельны
значит получается параллелограмм KBCD , где противоположные стороны попарно равны
BC = KD = 5см
по условию AK=6 см
тогда нижнеее основание AD = AK+KD =6+5 =11 см
средняя линия трапеции L = (AD +BC) / 2 = (11+5 ) /2 = 16 /2 = 8 см
ОТВЕТ 8 см