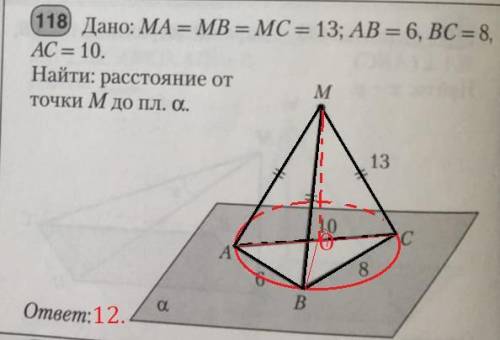
Точка M, равноудалена от вершин треугольника ABC, поэтому она лежит на перпендикуляре к (ABC), который восстановлен из центра (O) описанной около ΔABC окружности. Треугольник со сторонами 6, 8, 10 является египетским (10²=6²+8²), поэтому ∠B=90°, а значит центр описанной лежит на середине AC. И её радиус равен AC:2=10:2=5.
Как было сказано ранее MO⊥(ABC).
Рассмотри прямоугольный ΔAOM (∠O=90°): AO=5; AM=13. Найдём второй катет MO (расстояние от M до α) по теореме Пифагора (хотя тут опять Пифагорова тройка 5, 12, 13).
MO=√(13²-5²) = √((13+5)(13-5)) = √(18·8) = √(3²·4²) = 12
ответ: 12.
Объяснение длинное, зато решение очень короткое.
Проведем плоскость через диагональ параллелепипеда и ребра, с которыми она пересекается.
Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.
Ребра параллелепипеда параллельны между собой. Следовательно, раз данное ребро параллельно прямой на плоскости, содержащей диагональ параллелепипеда, оно параллельно и самой этой плоскости.
Рассмотрим рисунок.
Ребро и диагональ не параллельны между собой.
Прямые, которые не имеют общих точек и не параллельны, называются скрещивающимися.
Расстояние между скрещивающимися прямыми - это расстояние между одной из скрещивающихся прямых, в данном случае ребром параллелепипеда, и плоскостью, проходящей через другую прямую - диагональ параллелепипеда - параллельно этому ребру.
Для того, чтобы найти расстояние между двумя данными в задаче скрещивающимися прямыми, нужно:
из любой точки ребра опустить перпендикуляр на плоскость, содержащую диагональ параллелпепипеда, и найти длину этого перпендикуляра. . На данном рисунке - это расстояние mn=m1n1
Но расстояние m1n1- это половина диагонали прямоугольника, лежащего в основании параллелепипеда.
Половину диагонали параллелепипеда найдем по тепореме Пифагора:
m1n1=1/2 √(а²+b²)
ответ: расстояние равно 1/2 √(а²+b²)