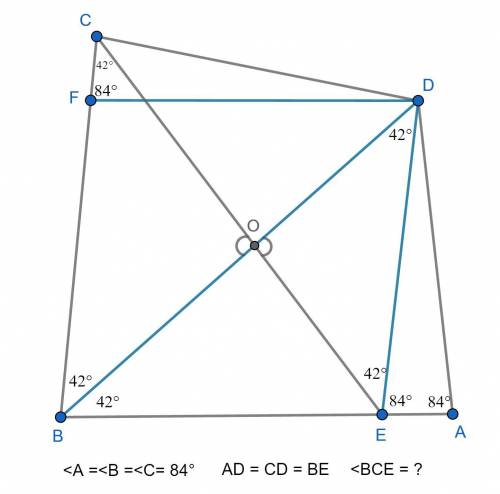
Через тч.D проведем прямую DF ║ BA. Соединим отрезком тч.D и тч.E.
∠DFC = ∠ABC = 84°, как соответствующие при DF ║ BA и CB секущей.
В ΔDFC ∠C=∠F = 84° ⇒ ΔDFC равнобедренный.
CD = FD = BE. (CD = BE по условию).
Так как FD и BE ║ и равны, то DFBE параллелограмм. ⇒ DE║FB.
∠DEA = ∠FBE = 84° как соответствующие при DE ║ FB и AB секущей.
В ΔDEA ∠E=∠A = 84° ⇒ ΔDEA равнобедренный, DE=DA = BE (DA = BE по условию).
⇒ BFDE ромб, ∠FBE = FDE = 84°, его диагональ BD является биссектрисой этих углов. ∠BDE = 42°.
BCDE - равнобедренная трапеция, углы при основаниях попарно равны. Тч. O является вершиной двух равнобедренных подобных треугольников.
ΔEOD подобен ΔCOB по двум углам. ∠COB = ∠EOD - вертикальные, ∠CBO = ∠ODE = 42°.
Из подобия треугольников следует равенство углов ∠BCO= ∠ODE = 42°.
∠BCE = 42°.
из вершины В опустить перпендикуляры на плоскость альфа (пересечет в точке Д) и на сторону АС (точка Е). Получим прямоугольный треугольник ВДЕ с острым углом ВЕД=30град и гипотенузой ВЕ. ВЕ- высота к АС в треугольнике АВС. Ее можно найти из формулы площади h=2S/AC S=V(h*(p-a)*(p-b)*(p-c)) p=1/2 *(a+b+c)=1/2 *(15+13+4)=16
S=V(16* (16-15)*(16-13)*(16-4))=V(16*1*3*12)=24
h=2*24/4=12
ВД-катет. лежащий напротив угла 30град и равен половине гипотенузы 1/2 *12=6
Расстояние от вершины В до плоскости альфа 6см
AМ= 14 см
MK= 14 см
KB= 28 см
Объяснение:
Точка К является серединой отрезка AB, то AК=КB=1/2*AB= 56 /2= 28 см;
Точка М является серединой отрезка AК, то AМ=МК=1/2*AК= 28 /2=14 см;
Если что-то непонятно, пишите в комментах.
Успехов в учёбе! justDavid