ЕСли АВСД - прямоугольник,
1)значит пара сторон(векторов) параллельны АВ(3-4;5-1)=АВ(-1;4)
ДС(-1-0;4-0)=ДС(-1;4)
Чтобы найти координаты вектора из координат конца вектора вычел координаты начала АВ=ДС (это векторы) раз координаты векторов равны то и векторы равны значит параллельны
2)Диагонали прямоугольника равны) - это уже длины
Сначала найду координаты векторов: АС(-1-4;4-1)=АС(-5;3)
ВД(0-3;0-5) =ВД(-3;-5)
Теперь найду длину АС=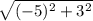 =
=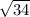 ВД=
ВД=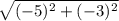 =
=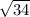
Так как АВ|| ДС; AB= СД; АС=ВД - это АВСД прямоугольник
Объяснение:
ответ: √(x² + y²)
Объяснение:
Расстояние между двумя точками -- это отрезок, соединяющий эти точки.
Воспользуемся формулой нахождения расстояния между двумя точками.
Пусть А(a₁; a₂), B(b₁, b₂), тогда
В нашем случае даны точки O(0; 0) и M(x; y). Подставим их координаты в формулу:
Воспользуемся координатной плоскость и теоремой Пифагора.
Изобразим на координатной плоскости точки O(0; 0) и M(x; y). Соединим их. Затем опустим перпендикуляры от точки М на ось ОХ и OY, обозначим получившиеся точки N(x; 0) и K(0; y).
(координатная плоскость во вложениях)
Получаем следующее: длина отрезка OK равна y - 0 = y, ON = x.
Также MN = OK = y
Рассмотрим ΔMNO. Он прямоугольный. Применим к нему теорему Пифагора и выразим гипотенузу OM: