1. Знайдіть довжину відрізка АВ і координати його середини, якщо А(4;-5) i B(-3;-1).
2. Складіть рівняння кола, центр якого знаходиться в точці
M(1;-3) і радіусом 7.
3. Складіть рівняння прямої, яка проходить через точки M-2-2)
і Р(2;10).
4. Складіть рівняння прямої, яка проходить через точку А-43)
і утворює з додатним напрямом осі абсцис кут 60.
5. Знайдіть координати точки, яка належить осі ординат і
рівновіддалена від точок С(2;-1) i B(-3;7).
6. Складіть рівняння прямої, яка паралельна прямій
y = 5х – 9 і проходить через центр кола
х' +y2 - 6х + 2 +6= 0.

👇

Увидеть ответ

Ответ:

super123jack

13.03.2023

а это на каком языке

4,6(63 оценок)

Открыть все ответы

Ответ:

Xopccc13377

13.03.2023

ответ:

$27\sqrt{3}$ ед².

Объяснение:

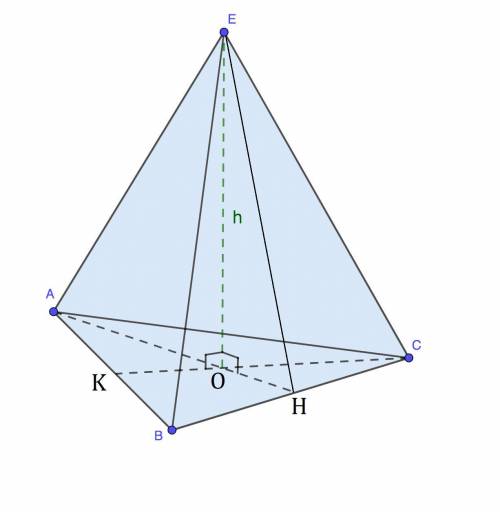
Обозначим данную пирамиду буквами 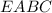EABC .

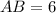AB=6 ед.

Проведём высоту 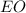. Точка 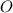- центр 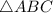$\triangle ABC$ - точка пересечения, медиан, высот и биссектрис треугольника.

Проведём апофему 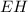(апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне 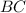основания пирамиды.

Т.к. данная пирамида - правильная, треугольная ⇒ основание пирамиды - правильный треугольник.

$\Rightarrow AB = BC = AC = 6$ .

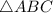Проведём высоту в $\triangle ABC$ .

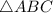Т.к. $\triangle ABC$ - равносторонний ⇒ - высота, медиана, биссектриса.

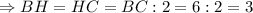
$\Rightarrow BH = HC = BC:2 = 6:2 = 3$

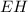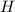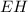Высота и апофема имеют общее основание, а именно точку , т.к. - медиана, а апофема делит 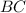пополам (по свойству).

$\angle EHO = 60^{\circ}$ .

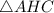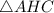Рассмотрим $\triangle AHC$ :

$\triangle AHC$ - прямоугольный, так как - высота.

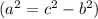
Найдём высоту по теореме Пифагора: (a^2 = c^2 - b^2)

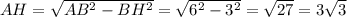$AH = \sqrt{AB^2 - BH^2} = \sqrt{6^2 - 3^2} = \sqrt{27} = 3\sqrt{3}$ ед.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Точка O - пересечение медиан и делит их в отношении 2 : 1, считая от вершины.

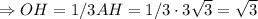$\Rightarrow OH = 1/3AH = 1/3 \cdot 3\sqrt{3} = \sqrt{3}$ ед.

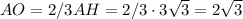$AO = 2/3AH = 2/3 \cdot 3\sqrt{3} = 2\sqrt{3}$ ед.

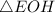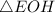Рассмотрим $\triangle EOH$ :

$\triangle EOH$ - прямоугольный, так как 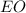- высота.

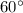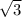Если угол прямоугольного треугольника равен $60^{\circ}$ , то напротив лежащий катет равен произведению меньшего катета на $\sqrt{3}$ .

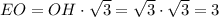$EO = OH \cdot \sqrt{3} = \sqrt{3} \cdot \sqrt{3}= 3$ ед.

Найдём апофему по теореме Пифагора: 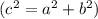(c^2 = a^2 + b^2)

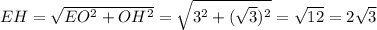$EH = \sqrt{EO^2 + OH^2} = \sqrt{3^2 + (\sqrt{3})^2} = \sqrt{12} = 2\sqrt{3}$ ед.

====================================================

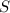полн. поверх. = S основ. + S бок.поверх.

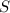осн. = $S_{\triangle ABC} = \dfrac{AB^2\sqrt{3}}{4} = \dfrac{6^2\sqrt{3}}{4} = 9\sqrt{3}$ ед².

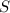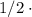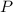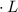бок. поверх. = $1/2 \: \cdot$ ( осн. $\cdot \: L$ ), где - апофема.

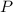осн. = AB + BC + AC = 6 + 6 + 6 = 18 ед.

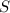⇒ бок. поверх. = 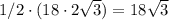$1/2\cdot(18 \cdot 2\sqrt{3}) = 18\sqrt{3}$ ед².

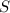⇒ полн. поверх. = $9\sqrt{3} + 18\sqrt{3} = 27\sqrt{3}$ ед².

сторона основания правильной треугольной пирамиды равна 6 боковая грань наклонена к плоскости основа

4,7(15 оценок)

Ответ:

IbraevaLisa

13.03.2023

Основание равнобедренного треугольника относится к его высоте, проведенной к основанию, как 3 : 2, боковая сторона треугольника равна 20 см. Найдите периметр треугольника (в см).

Объяснение:

Δ АВС, АВ=ВС=20 см, ВН-высота, АС:ВН=3:2 . Р-?

Высота в равнобедренном треугольнике является медианой, значит АН=НС.

Пусть АН=х см, АС=2х см ⇒ (2АН) :ВН=3:2 , ( 2х):ВН=3:2 ,ВН=(4х)/3.

ΔАВН-прямоугольный, по т. Пифагора АВ²=АН²+ВН² ,

400=х²+(16х²)/9 , (25х²)/9=400 , х²=144 , х=12.

АС=2*12=24 (см)

Р=20+20+24=64(см)

4,6(32 оценок)

Это интересно:

Компьютеры-и-электроника

06.09.2021