Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:
AB(1-2,-2-4,3-5)=AB(-1,-6,-2)
BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)
AC(-1-2,-2-4,4-5)=AC(-3,-6,1)
Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:
Опускаем Высоту СН на АВ. СН = sin В * 3 корня из 2 = sin 30 * 3корня из 2 = 0,5*3 корня из 2 = 1,5 корня из 2 НВ в квадрате = (3 корня из 2) в квадрате - (1,5 корня из 2)в квадрате = 9*2 - 9/2= 13,5 НВ = корень из 13,5 = 3 корня из 1,5 АН = СН= 1,5 корня из 2 так как треугольник равнобедренный (углы при основании АС равны 45). АВ = АН + НВ = 1,5 корня из 2 + 3 корня из 1,5 АС = корень из (АН в квадрате + СН в квадрате) = корень из (4,5+4,5)=3
ОТВЕТ угол А = 45 АВ= 1,5 корня из 2 + 3 корня из 1,5 АС=3
а)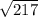
б)-28
Объяснение:
Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:
AB(1-2,-2-4,3-5)=AB(-1,-6,-2)
BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)
AC(-1-2,-2-4,4-5)=AC(-3,-6,1)
Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:
a=3AB-4AC=(3*(-1)-4*(-3),3*(-6)-4*(-6),3*(-2)-4*1)=(9,6,-10)
Длина вектора a - среднее квадратичное его координат:
|a|=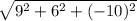 =
=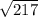
Формула скалярного произведения векторов a(a1,a2,a3) и b(b1,b2,b3) - ab=a1*b1+a2*b2+a3*c3
Итого ab=9*(-2)+6*0+(-10)*1=-28