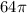см³.
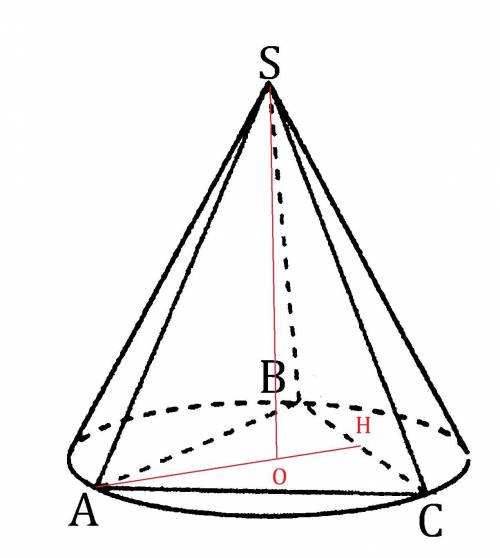
Обозначим данную пирамиду буквами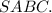 
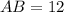см.
Проведём высоту пирамиды SO.
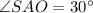
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
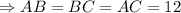см.
Проведём высоту 
в 
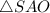- прямоугольный, так как 
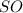- высота пирамиды.
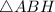- прямоугольный, так как - высота .
Так как - равносторонний ⇒ - высота, медиана и биссектриса
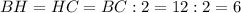см, так как - медиана.
Найдём по теореме Пифагора 
.
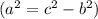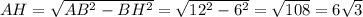см.
Точка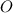 
- пересечение медиан и делит их в отношении 
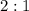, считая от вершины.
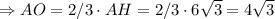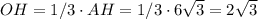см
см.
Также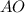 
- радиус описанной около окружности.
Рассмотрим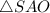
Если угол в прямоугольном треугольнике равен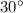 
, то напротив лежащий катет равен половине гипотенузы.
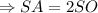
Составим уравнение:
Пусть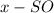 
, тогда 
.
И по теореме Пифагора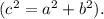 
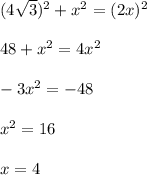
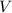конуса = 
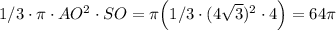см³.
234
Объяснение:
Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.
Угол BDA равен углу DBC как накрестлежащий. Следовательно CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.
Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.
Нужно найти катет HD.
Используем формулу для нахождения гипотенузы в прямоугольном треугольнике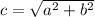
Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.
Найдем площадь трапеции по формуле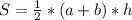
S=1/2*(15+24)*12=6*39=234