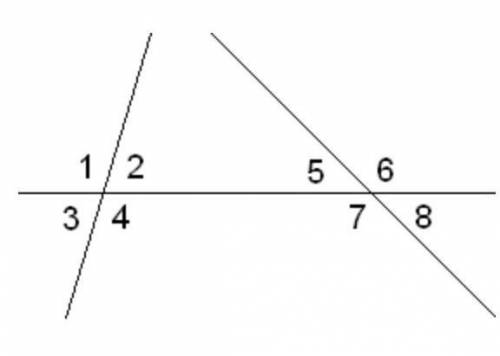
1)Треугольники подобны ⇒ и у другого треугольника стороныотносятся как 3х/4х/5х. Большая сторона - 5х, и она равна 15.
15=5х
х=3
тогда первая сторона 3х=9, вторая 4х=12
Периметр равен:9+12+15=36
ответ:36
2)Больший катет лежит против большего отрезка гипотенузы. По свойству катет в прямоугольном треугольнике есть среднее геометрическое между гипотенузой (16+9=25см) и его проекцией на гипотенузу (16см)
х=√(25*16)=20см
ответ:20см
3)Рисунок внизу.
В ΔABD по теореме косинусов:
cosABC=(AB²+BD²-AD²)/(2AB*BD)=(16+1-12,25)/(2*4*1)=4,75/8
В ΔABC по теореме косинусов:
AC²=AB²+BC²-2*AB*BC*cosABC=16+256-2*4*16*4,75/8=196
AC=14
ответ:14
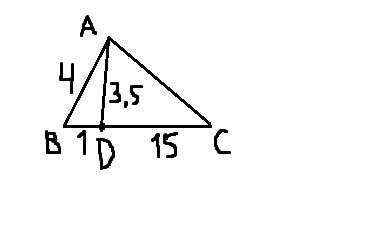
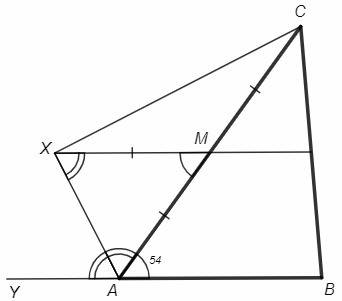
∠YAC - внешний угол, M - середина AC
∠YAX=∠MAX (AX - биссектриса ∠YAC)
∠YAX=∠MXA (накрест лежащие при XM||AB)
∠MAX=∠MXA => △XMA - равнобедренный, XM=MA
XM=MC, △XMC - равнобедренный => ∠XCA=∠MXC
∠XMA=2∠XCA (внешний угол равен сумме внутренних, не смежных с ним)
∠XMA=∠CAB=54 (накрест лежащие при XM||AB)
∠XCA=∠XMA/2 =54/2 =27
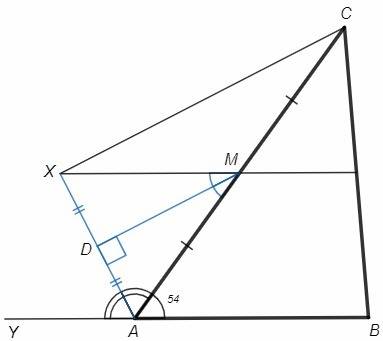
Или проведем биссектрису MD угла XMA. Биссектрисы внутренних углов при параллельных перпендикулярны, MD⊥AX. Биссектриса MD является высотой, следовательно и медианой. MD - средняя линия в треугольнике CAX, MD||CX. ∠XCA=∠DMA как соответственные. ∠XMA=∠CAB как накрест лежащие при XM||AB. ∠XCA=∠XMA/2=∠CAB/2=27
Объяснение:
13248481321324848132