а) По определению проекция фигуры на плоскость - совокупность проекций всех точек этой фигуры на плоскость проекции.
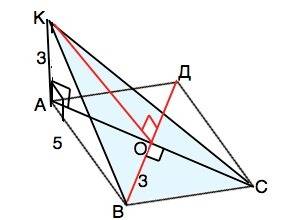
Точка К проецируется в основание перпендикуляра КА, т.е. в т. А.
Т. В и С ∆ КВС лежат в плоскости ромба. Через две точки можно провести только одну прямую. ⇒
Все точки сторон ∆ КВС проецируются на стороны ∆ АВС. ⇒
∆ АВС проекция ∆ КВС на плоскость ромба АВCД.
б) КА перпендикулярен плоскости ромба, следовательно, перпендикулярен любой прямой, проходящей в этой плоскости через т. А. ⇒КА⊥АС
Диагонали ромба взаимно перпендикулярны.⇒АС⊥ВД
АО - высота равнобедренного ∆ АВД. Из ∆ АОВ по т.Пифагора АО=√(B²-BO²)=√(25-9)=4
Расстояние от точки до прямой равно длине проведенного между ними перпендикуляра.
КО по т. о 3-х перпендикулярах перпендикулярен ВД.
Из прямоугольного ∆ КАО расстояние КО=√(КА²+АО*)=√(9+16)=5 см
Расстояние от точки до сторон квадрата равно 13 см. Найдите расстояние от точки до плоскости квадрата, если сторона квадрата равна 10 см. можете объяснить, с рисунком
Объяснение:
Расстояние от точки Т до плоскости отрезок ТО ⊥ ( АВС) . Значит ТО перпендикулярен любой прямой лежащей в плоскости.
Т.к. расстояние -это перпендикуляр, то опустим перпендикуляры из точки Т на стороны квадрата : ТН₁ , ТН₂ , ТН₃ , ТН₄. Тогда прямоугольные треугольники ( на рисунке желтые) равны по катету и гипотенузе ( апофема боковой грани).⇒точка О -центр вписанной окружности и еще т. пересечения диагоналей квадрата.
Н₁ Н₃= 10 , ОН₁=5 , из ΔТОН₁ , по т. Пифагора ТО=√(13³-5²)=√144=12 (см)