Рисунок к вопросу не был приложен, поэтому возможно пирамида выглядит по другому, но построения нужной точки остаётся правильным.
B,O∈(ABC); BO⊂(ABC); AC⊂(ABC). Пусть BO∩AC=P. *по рисунку O - лежит в треугольнике, поэтому прямые BO и AC не могут быть параллельными, а раз они лежат в одной плоскости, то они пересекаются.
O∈BP⊂(SBP) ⇒ O∈(SBP). O∈l; l║SB; SB⊂(SBP) из всего этого следует, что l⊂(SBP). SP⊂(SBP)
Ну и желательно оговорить почему прямые l и SP не параллельны. l⊥(ABC), BP⊂(ABC) ⇒ l⊥BP. Если l║SP, то SP⊥BP поскольку P∈BP. Получается, что из вершины S проведены две не совпадающие высоты к одной плоскости (ABC), что не возможно. Как итог l не параллельно SP, а раз они лежат в одной плоскости (SBP), то они пересекаются.
Пусть l∩SP=T. T - искомая точка, поскольку T∈SP⊂(SAC)
ответ: l∩(SAC)=T.
Это было доказательство того, что построение верное.
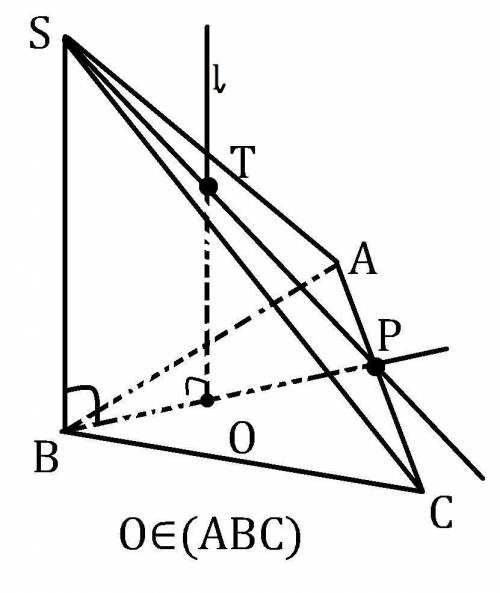
Рисунок к вопросу не был приложен, поэтому возможно пирамида выглядит по другому, но построения нужной точки остаётся правильным.
B,O∈(ABC); BO⊂(ABC); AC⊂(ABC). Пусть BO∩AC=P. *по рисунку O - лежит в треугольнике, поэтому прямые BO и AC не могут быть параллельными, а раз они лежат в одной плоскости, то они пересекаются.
O∈BP⊂(SBP) ⇒ O∈(SBP). O∈l; l║SB; SB⊂(SBP) из всего этого следует, что l⊂(SBP). SP⊂(SBP)
Ну и желательно оговорить почему прямые l и SP не параллельны. l⊥(ABC), BP⊂(ABC) ⇒ l⊥BP. Если l║SP, то SP⊥BP поскольку P∈BP. Получается, что из вершины S проведены две не совпадающие высоты к одной плоскости (ABC), что не возможно. Как итог l не параллельно SP, а раз они лежат в одной плоскости (SBP), то они пересекаются.
Пусть l∩SP=T. T - искомая точка, поскольку T∈SP⊂(SAC)
ответ: l∩(SAC)=T.
Это было доказательство того, что построение верное.

Задача на свойство отрезков касательных, проведенных из одной точки к одной окружности, отрезки таких касательных до точек касания равны, поэтому, если коэффициент пропорциональности равен х, х>0, то боковые стороны по (8х+3х), а основание (8х+8х)
Составим и решим уравнение.
2*11х+16х=76
38х=76
х=76/38
х=2
тогда боковые стороны по 2*11=22 /см/, а основание 16*2=32/ см/
ответ 22см; 22см;32см.