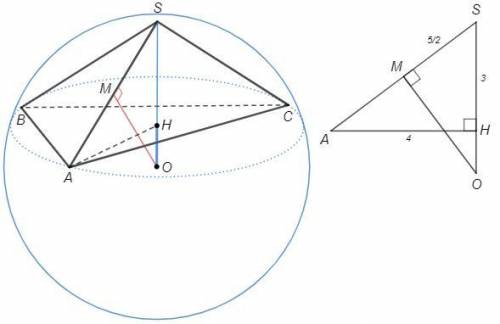
Основание ABC, AB=4, ∠C=30°
H - центр описанной окружности.
AB/sinC =2AH (т синусов) => AH=4
Если боковые ребра пирамиды равны, то вершина падает в центр описанной окружности основания.
SH⊥(ABC)
SH=√(SA^2-AH^2) =3 (т Пифагора)
О - центр описанной сферы.
OABC - пирамида с равными боковыми ребрами, следовательно ее вершина также падает в центр H.
OH⊥(ABC)
S-H-O на одной прямой.
В плоскости ASO.
OS=OA, О на серединном перпендикуляре к SA.
M - середина SA, SM=5/2
△SOM~△SAH
SO/SA=SM/SH => SO/5=5/2*3 => SO=25/6
OH =SO-SH =25/6 -3 =7/6
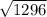 =36
=36
Дано: А(5;-1), В(1;2)
Найти: координаты вектора АВ и |AB|
1) Вектор АВ={х2-х1; у2-у1};
Вектор АВ={1-5; 2-(-1)};
Вектор АВ=(-4; 3);
2) |AB|=√x^2+y^2;
|AB|=√(-4)^2+3^2:
|AB|=√16+9;
|AB|=√25;
|AB|=5
ответ: Вектор АВ (-4;3), |AB|=5