Объяснение: задание 1
Длину отрезков найдём по формуле: √(х1-х2)²+√(у1-у2)². Найдём сторону АВ:
АВ=√(-1-3)²+√(1-1)²=√(-4)²=√16=4
Найдём сторону СД, она должна быть равна АВ:
СД=√(3+1)²+√(-2+2)²=√4²=√16=4
Итак: стороны АВ=СД=4
Найдём другие две стороны ВС и АД:
ВС=√(3-3)²+√(1+2)²=√3²=3
АД=√(-1+1)²+√(1+2)²=√3²=3
Итак: ВС=АД=3.
Теперь найдём площадь прямоугольника зная его стороны по формуле: S=a×b, где а и b –стороны прямоугольника:
S=3×4=12
S=12
ЗАДАНИЕ 2
Найдём таким же образом длину диаметра MN:
MN=√(-2-2)²+√(2-2)²=√(-4)²=√16=4
Диаметр MN=4. Теперь найдём длину окружности, зная длину диаметра по формуле L= 2πr, где L - длина окружности, r- её радиус умноженный на 2, т. е. диаметр:
L=π×4=12,56;
ответ: L=12,56
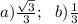
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
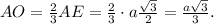
Угол между прямой SA и плоскостью АВС есть угол SAO
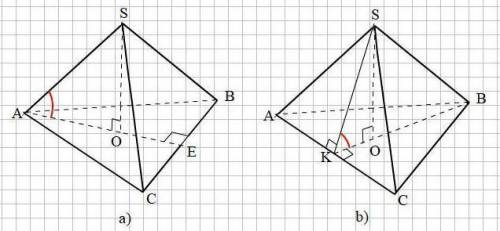
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
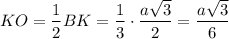
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
Через точку А отрезка АВ проведена плоскость α. Через точки В и середину М отрезка АВ проведены параллельные прямые, пересекающие плоскость α в точках В1 , М1 соответственно.
Найдите длину отрезка ММ1 , если ВВ1 =12м.
Объяснение:
Плоскости α и (ВАВ₁) пересекаются по прямой АВ₁ .
ΔАММ₁ подобен ΔАВВ₁ по 2 углам :∠А-общий, ∠АММ₁=∠АВВ₁ как соответственные , т.к. ММ₁║ВВ₁, АВ-секущая ⇒ сходственные стороны
пропорциональны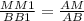 , учитывая что АВ=2АМ , получаем
, учитывая что АВ=2АМ , получаем