Радиус вписанной в прямоугольный треугольник окружности находят по формуле:
r=(а+b-c):2,
где а, в - катеты, с - гипотенуза треугольника
Радиус и сумма катетов даны в условии задачи.
2=(а+b-c):2
4= 17-c
с=17-4
с=13 см - это длина гипотенузы.
Периметр равен 13+17=30 см
Можно заметить, что стороны этого треугольника из Пифагоровых троек, и они равны 5, 12,13. , т.к. их сумма 17.
При желании каждый сможет в этом убедиться, применив теорему Пифагора.
Площадь треугольника
S=12*5:2=30 cм²
Не все и не всегда мы помним о пифагоровых тройках.
Когда известен периметр многоугольника и радиус вписанной в него окружности, площадь можно найти иначе - умножив половину периметра на радиус вписанной окружности, что в итоге даст тот же результат:
S= 30:2*2=30 см²
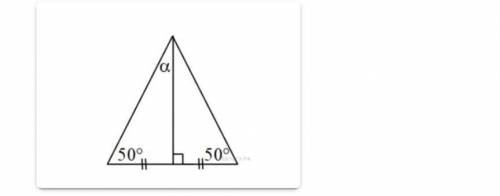
угол а равен 80 градусов
Объяснение:
сумма внутренних углов треугольника равна 180°
большой треугольник состоит из 2 маленьких
углы маленького треугольника равны 50 и 90 градусов
третий угол маленького треугольника равен 180-(50+90)=40°
угол а состоит из двух углов маленького треугольника с градусной мерой 40°
сам угол а будет равняться 40+40 или 40·2 80°
чтобы проверить, так ли это, сложим все градусные меры улов большого треугольника: 50+50+80=180°