4√3 см
Объяснение:
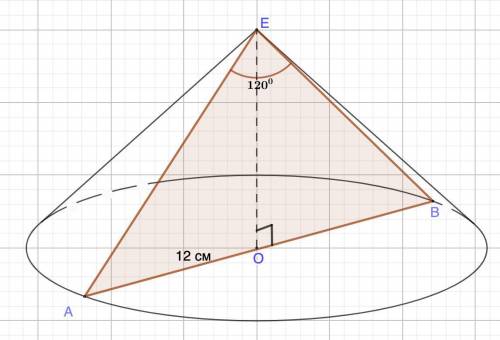
Дано: конус.
АЕВ - осевое сечение.
∠АЕВ = 120°
АО = 12 см - радиус основания.
Найти: ЕО
Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого – образующие, а основание – диаметр основания конуса.⇒ ΔАЕВ - равнобедренный.
В равнобедренном треугольнике высота , проведенная к основанию, является биссектрисой.⇒ ∠АЕО = ∠ОЕВ = 120°:2 = 60°
Рассмотрим ΔАЕО - прямоугольный.
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠ЕАО = 90° - °АЕО = 90° - 60° = 30°
Пусть ОЕ = х см
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ АЕ = 2х см
По теореме Пифагора:
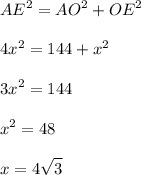
⇒ ЕО = 4√3 см
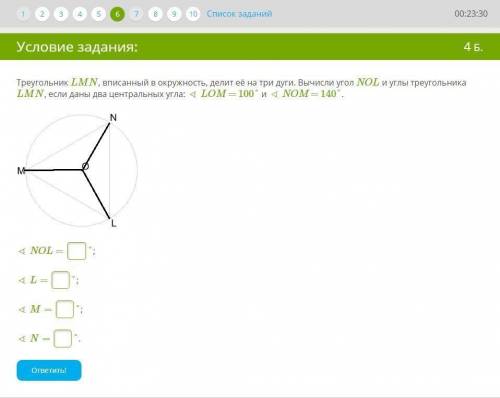
ответ: ∠NOL=120°, ∠L=70°, ∠М=60°, ∠N=50°
Объяснение:
1) ∠NOL + ∠LOM + ∠NOM = 360° (т.к. окружность)
∠NOL + 100° + 140° = 360°
∠NOL = 360° - (100° + 140°) = 120°
2) ∠N = ∠MON + ∠ONL
∠M = ∠NMO + ∠LMO
∠L = ∠MLO + ∠NLO
3) Рассмотрим треугольник MON:
MO = ON (т.к. радиусы) ⇒
треугольник MON - равнобедренный ⇒
∠MNO = ∠OMN
∠MON + ∠MNO + ∠OMN = 180° (по сумме углов треугольника)
140° + ∠MNO + ∠MNO = 180°
2×∠MNO = 180° - 140°
∠MNO = 40° / 2 = 20°
∠MNO = ∠OMN = 20°
Аналогично находим углы ONL(30°), OLN(30°), OLM(40°), OML(40°)
4) из п. 2 и п. 3 имеем:
∠N = ∠MNО + ∠ONL = 20° + 30° = 50°
∠M = ∠NMO + ∠LMO = 20° + 40° = 60°
∠L = ∠MLO + ∠NLO = 40° + 30° = 70°
1)Так как AK является биссектрисой, угол BAK = угол KAD = 60/2 = 30°.
Сумма односторонних углов трапеции = 180°, следовательно, угол ABK = 180 - 60 = 120°
2) Рассмотрим треугольник ABK.
Нам известно, что угол BAK = 30°, угол ABK = 120°, а сумма углов треугольника = 180°, следовательно, угол BKA = 180 - угол ABK - угол BAK = 30°. Угол BAK = угол BKA, следовательно, треугольник BAK - равнобедренный.
3) Если BC = 16, то BK = AB = 8. Так как ABCD - равнобедренная трапеция, то AB = CD = 8, угол BAD = угол CDA.
4) Проведем высоты BH и CP.
Рассмотрим треугольники ABH и DCP
Углы ABH и DCP равны 30°, так как сумма углов треугольника равна 180°
Свойство 30° в прямоугольном треугольнике: если в прямоугольном треугольнике присутствует угол, равный 30°, то катет, который лежит напротив этого угла, равен половине гипотенузы. Следовательно, AH = DP = 8/2 = 4.
5) Рассмотрим BHPC
Так как BC || AD (основания у трапеции параллельны), BH || CP(они оба перпендикулярны стороне AD, следовательно, параллельны друг другу), BHPC - прямоугольник, следовательно, BC = HP = 16.
Найдем AD: AD =AH + HP + PD = 4 + 16 + 4 = 24.
ответ: 24.