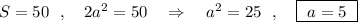6 см
Объяснение:
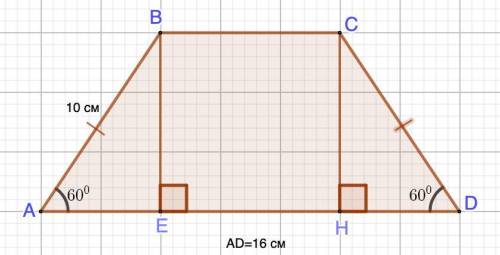
Дано: ABCD - равнобедренная трапеция.
АВ=СD=10 см; АD=16 см;
∠А=∠D=60°
Найти: АD
ВЕ и СН - высоты.
Рассмотрим ΔАВЕ - прямоугольный (построение)
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠АВЕ=90°-60°=30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒АЕ = 10:2=5 (см)
Аналогично в ΔНВD:
НD=5 см
⇒ ЕН=16-(5+5)=6 (см)
Если две прямые перпендикулярны третьей, то эти прямые параллельны.
ВЕ⊥АD; СН⊥АD ⇒ВЕ║СН.
⇒ ЕВСН - параллелограмм.
У параллелограмма противоположные стороны равны.
⇒ ЕН=ВС=6 см
ответ: h=5 см .
АВСД - трапеция, АВ=СД , ∠А=∠Д=45° ,
ВС=а , ВН ⊥ АД , h=ВН=ВС=а , S(трап)=50см² .
Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
То есть ΔАВН - равнобедренный и АН=ВН=а .
Аналогично, из ΔСДМ получаем, что ДМ=СМ=а .
Тогда АД=АН+НМ+МД=а+а+а=3а .
Площадь трапеции :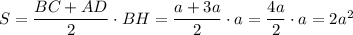
По условию: