ответ: 337,5 см²
Объяснение:
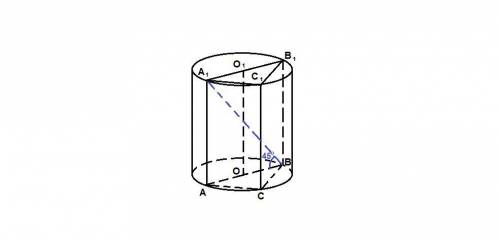
Так как цилиндр описан вокруг призмы, то основания призмы вписаны в основания цилиндра, боковое ребро призмы является высотой цилиндра.
Площадь полной поверхности цилиндра - это сумма площади боковой поверхности и площади двух оснований:
Sпов = 2πRh + 2 · πR²
Центр окружности, описанной около прямоугольного треугольника лежит на середине гипотенузы. Значит, радиус основания цилиндра равен половине гипотенузы:
ΔАВС: ∠С = 90°, по теореме Пифагора:
АВ = √(АС² + ВС²) = √(9² + 12²) = √(81 + 144) = √225 = 15 см
R = 1/2 AB = 7,5 см
Большая грань призмы - грань, содержащая гипотенузу основания.
Так как диагональ прямоугольника АВВ₁А₁ делит прямой угол пополам, то АВВ₁А₁ - квадрат. Тогда
h = AA₁ = AB = 15 см
Sпов = 2πRh + 2 · πR² = 2π · 7,5 · 15 + 2π · 7,5² =
= 225π + 112,5π = 337,5π см²
Объяснение:
возьмем одно основание за х , тогда другое будет 2х
(х+2х)/2=30
3х/2=30
3х=60
х=20 (одно основание)
2×20=40 (второе основание трапеции)