
1.это все вложения( первые 4)
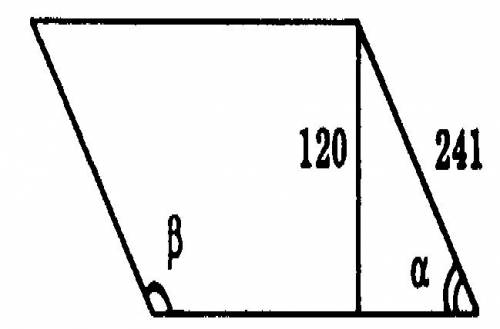
2.Пусть в треугольнике АВС высота АН; АН=12.4 ВС=40.6 Следовательно ВН=НС=20.3 По т. Пифагора АВ^2=AC^2=ВН^2+AH^2 ; АВ=23.8=АС
(
3.
cosa=5\13; тогда
sin^2a = 1-(5\13)^2 = sina = корень из (1-(5\13)^2 )= корень из (144\169) =12\13
sina=12\13
тогда ctga= cosa\sina = (5\13)\(12\13)=5\12
и tga= sina\cosa = (12\13)\5\13=12\5
4.
cos в квадрате а + sin в квадрате а = 1
cos a = квадратный корень из 1 - sin в квадрате а
cos a = квадратный корень из 1 - 9/25 = 4/5
tg a = sin a/ cos a
tg a = 3/5 / 4/5 = 3/4
ctg a = 1/tg a= 4/3
P.S. я не знаю, в какой четверти а. Поэтому со знаками не могу
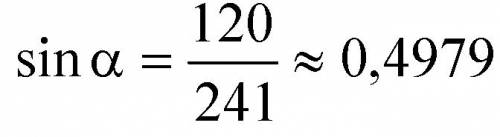
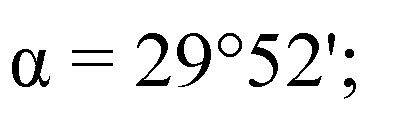

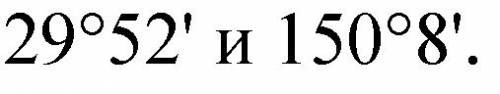
6 ед.
Объяснение:
В правильной усеченной пирамиде в основаниях лежат правильные многоугольники, стороны которых соответственно равны между собой. Боковые грани такой пирамиды - равные между собой равнобокие трапеции. Радиусы окружностей, вписанных в основания, проведенные в точки касания сторон оснований с соответственной окружностью Н и Н1, перпендикулярны к сторонам оснований по свойству радиусов, проведенных в точки касания.
Проведем перпендикуляр из точки касания Н1М верхнего основания на нижнее основание. Тогда отрезок Н1Н перпендикулярен стороне основания АВ по теореме о трех перпендикулярах, то есть является искомой высотой боковой грани.
В прямоугольном треугольнике НН1М угол ∠НН1М = 30° по сумме острых углов. Следовательно, НН1 = 2·НМ по свойству катета, лежащего против угла 30°.
НМ = ОН - О1Н1 = 8-5 = 3 ед.
Высота боковой грани НН1 = 6 ед.
Объяснение:
угол АОС =180=47=133
удачи