1. PM=KN, PN=KM. MN=MN
PMN=KMN, по ріності трьох сторін. Тоді ∠MPN=∠MKN.
∠PAM=∠KAN, як вертикальні. Тоді й ∠PMA=∠KNA.
MPA=AKN, за стороною PM і двома прилеглими кутами.
(А довести рівність трикутників AKM і BKM неможливо, таких трикутників на малюнку немає).
2. Умова жахлива і незрозуміла, але я спробую розібрати що до чого. Тож, як я розумію:
Відомо, що кут DCK =CKD.Знайдіть периметр трикутника DCK якщо він на 12 см більший за сторону DC.
Тож, маємо рівнобедрений трикутник CDK, основа СК.
DC=DК=х
DК+СК+DC=12+х
Далі не вистачає даних. Можу лише сказати, що сторона 7≤DC≤11. Тобто, Р (периметр DCK) 19≤Р≤23.
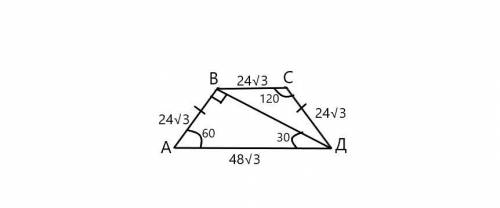
АВ=АД/2 (как катет лежащий против угла 30°) АВ=48√3/2=24√3; СД=АВ (трапеция равнобедренная); углы В и Д в треугольнике ВСД равны 30° (угол В в трапеции (180-60)=120°, угол В в треугольнике (120-90)=30°, угол Д в треугольнике (60-30)=30°); площадь трапеции равна сумме площадей треугольников АВД и ВСД; площадь треугольника равна половине произведения длин сторон на синус угла между ними.
S(АВД)=48√3*24√3*√3/4=864√3;
S(ВСД)=24√3*24√3*√3/4=432√3;
S(АВСД)=864√3+432√3=1296√3 ед².
Можно проще.
S(равнобедренной трапеции)=с*sinα(b-c*cosα), где b - основание , с - боковая сторона, α - угол при большем основании;
S=24√3*√3/2*(48√3-24√3/2)=36*36√3=1296√3 ед².
Еще можно через нахождение высоты, но думаю это лишнее.
Эту задачу легко можно решить "стандартными" методами, но на самом деле, ответ "периметр = 30" возникает мгновенно, если сообразить, что эта трапеция - половина правильного шестиугольника. Большое основание равно двум боковым сторонам, и все остальные стороны равны, всего периметр равен 5*боковая сторона, которая равна 6.
Если что-то не понятно, представьте правильный шестиугольник вписанным в окружность. Его стороны равны радиусу, а большая диагональ - диаметру. Трапеция, заданная в задаче - как раз половина правильного шестиугольника, ограниченная большой диагональю.
Сторону найти просто - это 6*корень(3)*ctg(60) = 6