АВСД, АС=6V2 ВД=8V2
диагонали делят ромб на 4 равных прямоугольных треугольника. АВО, СВО, АДО, СДО
точка О - точка пересечения диагоналей, которая делит каждую из них пополам
значит АО=СО и ВО=ДО
рассмотрим треугольник АВО:
АО=1/2АС= 3V2
ВО=1/2ВД= 4V2
п теореме Пифагора АО^2+BO^2=AB^2= (3V2)^2+(4V2)^2=50
АВ^2+BC^2+CД^2+ДА^2=4*AB^2=4*50=200
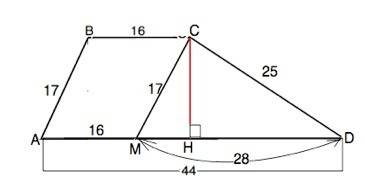
Назовем трапецию АВСD. АВ=17 см, ВС=16 см, СD=25 см, AD=44 см
Площадь трапеции равна произведению её высоты на полусумму оснований. Основания даны, высоту надо найти.
Один из решения:
Проведем СМ параллельно ВА. СМ=17 см (или ВК параллельно СD. Тогда ВК=25).
Получим треугольник, в котором известны три стороны: 17, 25 и 28 см.
По ф. Герона площадь этого треугольника равна 210 см².
Высота СН является и высотой трапеции.
S(∆ MCD)=CH•MD:2⇒
CH=2•S:MD=420:28=15 см
S(ABCD)=CH•(BC+AD):2=15•30=450 см²
Сумма квадратов диагоналей параллелограма равна суме квадратов всех его сторон
(6 х корень2) в квадрате + (8 х корень2) вквадрате = 72+128 =200
Сумма квадратов диагоналей =200