Прямые ОА и АС - являются секущими по отношению к данной окружности.
Объяснение:
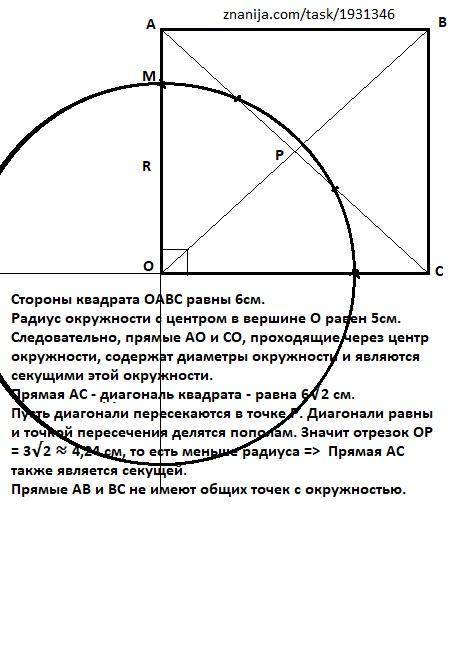
Стороны квадрата ОАВС равны 6см.
Радиус окружности с центром в вершине О равен 5см.
Следовательно, прямые АО и СО, проходящие через центр окружности, содержат диаметры окружности и являются секущими этой окружности.
Прямая АС - диагональ квадрата - равна 6√2 см.
Пусть диагонали пересекаются в точке Р. Диагонали равны и точкой пересечения делятся пополам. Значит отрезок ОР = 3√2 ≈ 4,24 см, то есть меньше радиуса => Прямая АС также является секущей.
Прямые АВ и ВС не имеют общих точек с окружностью.
а) ∠В = 30°, АВ=4 см, AD=ВD=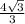
см ∠D=120°
б) S = 2√3 cм²
Объяснение:
а) Сумма острых углов прямоугольного треугольника равна 90°
∠В=90°-∠А=90°-60°=30°
Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.
⇒ АВ=2*АС=2*2=4см
По теореме Пифагора найдём катет ВС:
ВС = 2√3 см
Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.Рассмотрим ΔABD: ∠ВАD=30° - так как AD – биссектриса, ∠В=30° ⇒ ΔABD- равнобедренный, AD=ВD=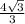
см
Так как сумма углов треугольника = 180°, то
∠АDB = 180-∠ВАD-∠В=180-30-30=120°
б) Площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2:
S = 2√3 cм²