Уравнение окружности радиуса R с центром в точке C (a; b) имеет вид:
(x – a)² + (y – b)² = R².
1. Радиус — расстояние от центра окружности до любойточки на окружности. Таким образом, радиус будет равен расстоянию от точки c (2; 1) до точки d (5; 5).
Расстояние между точками A (x₁; y₁) и B (x₂; y₂) вычисляется по формуле:
AB = √((x₁ - x₂)² + (y₁ - y₂)²).
Таким образом, расстояние между точками c (2; 1) и d (5; 5) будет равно:
cd = R = √((2 - 5)² + (1 - 5)²) = √((- 3)² + (- 4)²) = √(9 + 16) = √25 = 5.
1. Подставим известные значения в уравнение окружности радиуса R = 5 с центром в точке c (2; 1):
(x – 2)² + (y – 1)² = 5²;
(x – 2)² + (y – 1)² = 25.
ответ: (x – 2)² + (y – 1)² = 25.
Уравнение окружности радиуса R с центром в точке C (a; b) имеет вид:
(x – a)² + (y – b)² = R².
1. Радиус — расстояние от центра окружности до любойточки на окружности. Таким образом, радиус будет равен расстоянию от точки c (2; 1) до точки d (5; 5).
Расстояние между точками A (x₁; y₁) и B (x₂; y₂) вычисляется по формуле:
AB = √((x₁ - x₂)² + (y₁ - y₂)²).
Таким образом, расстояние между точками c (2; 1) и d (5; 5) будет равно:
cd = R = √((2 - 5)² + (1 - 5)²) = √((- 3)² + (- 4)²) = √(9 + 16) = √25 = 5.
1. Подставим известные значения в уравнение окружности радиуса R = 5 с центром в точке c (2; 1):
(x – 2)² + (y – 1)² = 5²;
(x – 2)² + (y – 1)² = 25.
ответ: (x – 2)² + (y – 1)² = 25.
Так как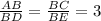 , то АС | | ЕD
, то АС | | ЕD
1) DE :AC=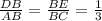
2)Периметры треугольников ABC и DEB относятся как коэффициент подобия, который равен числу 3