1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
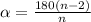
Найдем при каком n угол будет равен 160°:
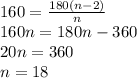
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
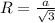
Подставим заданное значение стороны:
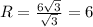
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
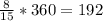 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см
1. Построй окружность,радиусом равным половине гипотенузы.Проведи диаметр окружности,он будет равен гипотенузе.Из конца этого диаметра отложи угол,равный данному острому углу,луч пересекает окружность в вершине искомого треугольника,осталось только соединить эту вершину с концами диаметра.
2. 1) начертить прямую и отметить на ней катет (длину)
2) От одного его края построить прямой угол, опустив перпендикуляр
3) от другого построить угол, равный углу, который дан
4) В месте, где стороны треугольника соединятся (которые от углов 90 и данного градуса) и буде 3 точка треугольника
вот и всё...
В этой трапеции наклонная боковая сторона, большее основание и меньшая диагональ составляют равносторонний треугольник, так как меньшая диагональ делит тупой угол трапеции на 2 угла по 60°. Это следует из того, что углы при боковой стороне трапеции в сумме составляют 180°.
180-60-60=60°.
Значит, угол меньшей диагонали и большего основания тоже равен 60°.
Опустив перпендикуляр из вершины тупого угла на основание, разделит его на 2 равные части по 6 см ( этот перпендикуляр - высота равностороннего треугольника, которая является и медианой). Следовательно, меньшая сторона равна 6 см.
Средняя линия трапеции - полусумма оснований - равна
(12+6):2=9 см