Углы при основании равны по 45°, угол при вершине 90°
Объяснение:
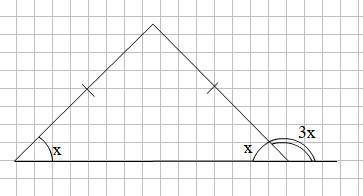
Пусть угол при основании равнобедренного треугольника равен х, тогда внешний угол при основании равнобедренного треугольника равен 3х.
Эти углы смежные, их сумма равна 180°.
х + 3х = 180°
4х = 180°
х = 45° - угол при основании
3х = 3 · 45° = 135° внешний угол при основании
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Внешний угол при основании равнобедренного треугольника равен 135°, один из не смежных с ним углов при основании равен 45°, тогда угол при вершине равен
135° - 45° = 90°.
1. <C=180°-(60°+45°)=75° (сумма внутренних углов треугольника равна 180°).
2. По теореме синусов ВС/sin60=DC/sin45, отсюда
CD=BC*Sin45/Sin60 =√3*(√2/2)*2/√3=√2.
3. ВС/sin60=BD/sin75.
Sin75=Sin(45+30)=Sin45*Cos30+Cos45*Sin30=
(√2*√3/4 + √2/4)=√2(√3+1)/4.
BD=BC*Sin75/Sin60=√3*(√2(√3+1)/4)*2/√3=√2(√3+1)/2.
ответ: <C=75°, BD=√2(√3+1)/2, CD=√2.
Проверка: площадь треугольника равна (1/2)*a*b*sinα.
S=(1/2)*√2*√3*(√2(√3+1)/4)=√3(√3+1)/4.
S=(1/2)*√2*(√2(√3+1)/2)*(√3/2)=√3(√3+1)/4.
S=(1/2)*(√2(√3+1)/2)*(√2/2)=√3(√3+1)/4.