1.Треугольник ABD = 1. Угол ВАD = CAD
2. BDA=CDA
треугольнику ADC
3.AD - общая сторона.
Второй признак равенства
треугольников
2.
Углы 1 и 2 вертикальные, значит они
равны, следовательно треугольники, по двум углам и стороне, равны. Исходя из этого, СD делиться попалам в точки О
3.
<АСО=<1 как вертикальные углы.
<BDO=<2 как вертикальные углы. Но
<1=<2, значит
<ACO=<BDO.
<AOC=<BOD как вертикальные углы.
Значит, треугольники АСО и BDO
равны по второму признаку: сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней
углам другого треугольника: - ОС=ОD по условию;
- <ACO=<BDO как доказано выше;
.<AOC=<BOD как доказано выше. У равных треугольников АСО и BDO равны соответственные углы А и В.
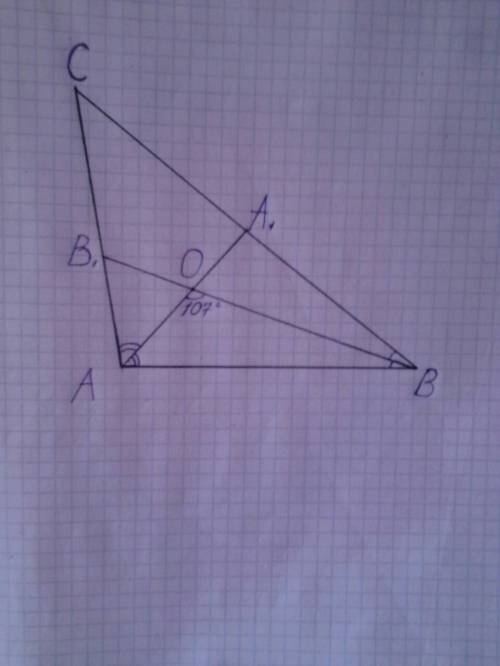
4.
Рассмотрим Δ АОВ. ∠AOB=107° - по условию. Так как ВВ1 биссектиса и делит угол АВС пополам ∠ АВО= 1/2∠АВС=1/2*30=15°
Сумма углов треугольника равна 180°. ∠ ОАВ=180-107-15=58°
Рассмотрим Δ АВС . Так как АА 1 биссектрисса и делит угол САВ пополам, ∠ САВ = 2*∠ОАВ=2*58=116°
∠ АСВ = 180-116-30= 34°
Остроугольный треугольник - это треугольник, в котором все три угла острые, т.е. меньше 90°.
В ΔABC два острых угла ∠ АВС=30 °, ∠АСВ=34 °, а ∠САВ=116 °. Значит ΔАВС не острый, а тупоугольный.
Острые углы (х,у) прямоугольного треугольника = (90=х+у); у=25+х. Следовательно:
90=х+25+х далее 65=2х, отсюда х=32.5, у=90-32.5=57.5 гр.
ответ: у=57.5 гр.