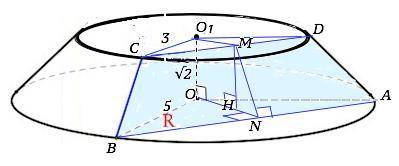
В усеченном конусе радиусы оснований равны 5 см и 3 см. Через две его образующие проведено сечение плоскостью, которая отсекает от оснований дуги по 120°. Найдите площадь (в см²) сечения, если высота усеченного конуса равна √2 см.
—————————
ответ: 12 см²
Объяснение: Основания усеченного конуса параллельны, его образующие равны,⇒ основания сечения лежат в параллельных плоскостях, а плоскость сечения является равнобедренной трапецией.
Радиусы оснований и хорды, соединяющая их концы, образуют равнобедренные треугольники АОВ и СО1D c углами при вершинах О и О1, равными величине отсекаемых плоскостью сечения дуг, т.е. 120°.
Из суммы углов треугольника острые углы этих треугольников (180°-120°):2=30°.
По т. синусов АВ:sin120°=ОВ:sin30°, откуда АВ=5√3.
Аналогично СD=3√3
По свойству катета, противолежащего углу 30°, катет О1М=0,5•О1С=3/2 см.
Аналогично ОN=0,5•ОВ=0,5•5=2,5 см.
Для нахождения высоты MN трапеции АВСD проведем высоты(медианы) О1М в ∆ СO1D и ON в ∆ ВOA и опустим из М перпендикуляр МН на ОN.
ОН⊥АВ ⇒ по т. о 3-х перпендикулярах MN⊥АВ. MN - высота сечения.
OH=O1M=1,5 см
НN=2,5-1,5=1 MH=O1O=√2 см
В прямоугольном треугольнике МНN по т.Пифагора МN=√(MN^2+NH^2)=√(2+1)=√3 см
Площадь трапеции равна произведению её высоты на полусумму оснований.
S(ABCD)=MN•(CD+AB)•1/2=(3√3+5√3)•1/2=12 (см²)
совершенно невыгодные именно для себя условия дуэли, при которых даже пустяковая рана должна обернуться смертью?
6. Как автор подчёркивает большое волнение Печорина, несмотря на внешнее спокойствие?
7. Печорин пристально наблюдает за Грушницким? Какие его переживания он отмечает с удовольствием, а какие его разочаровывают?
8. Каких действий ждёт от Грушницкого Печорин? В какие условия ставит Грушницкого для этого Печорин?
9. Какие чувства испытывает Печорин к Грушницкому перед своим выстрелом? Как герой пытается повлиять на Грушницкого?
10. Как перед своим выстрелом Печорин вновь пытается примириться с Грушницким? После каких его слов герой стреляет