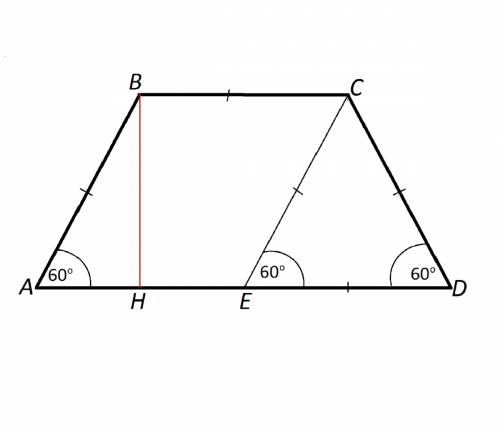
опускаем перпендикуляр из верхнех углов, они отсекают от нижней грани равные части, если верхняя основа = 6, 12-6=6, т.к. частей
этих 2, то делим на 2, значит одна из этих "отсекаемых" частей = 3. у нас получается треугольник, в котором, есть одно из этих частей нижней основы(3), нижний угол (60) и прямой угол (90), мы знаем что сумма углов треугольника равна 180, значит верхней угол будет = 180 - (60 +90)=30. за теоремой мы знаем что катет прямоугольного треугольника лежащий против 30 градусов, равен половине гепотенузы, а в нашем случаее это та самая отсекаемая часть (3), значит гипотенуза = 3 * 2 = 6. гипотенуза и есть боковая часть.
ответ боковая часть равно 6
Пусть нижнее основание равно а, верхнее равно b, боковая сторона равна с, угол при нижнем основании равен α.
У трапеции, в которую вписана окружность, боковая сторона равна средней линии: с = (a + b)/2.
Используем формулу площади трапеции:
S = ((a+b)/2)*h = ((a+b)/2)*√(ab).
Получаем первое уравнение: ((a+b)/2)*√(ab) = 576 или
(a+b)*√(ab) = 1152.
Теперь используем заданное условие: расстояние между точками касания этой окружности боковых сторон равно 3.
Выразим расстояние t между точками касания.
t = b+2(b/2)*cos α = b(1 + cos α) = 3.
Косинус альфа выразим так:
cos α = ((a - b)/2)/c = ((a - b)/2)/((a + b)/2) = (a - b)/(a + b).
Тогда второе уравнение получим в виде:
b(1 + ((a - b)/(a + b))) = 3.
Решаем систему из двух уравнений с неизвестными a и b.
{(a+b)*√(ab) = 1152.
{b(1 + ((a - b)/(a + b))) = 3.
Решение даёт значение оснований трапеции:
a = 12(√15 + 4) ≈ 94,4758.
b = -12(√15 - 4) ≈ 1,5242.
Находим радиус r вписанной окружности.
r = h/2 = √(ab)/2 = 6.
ответ: радиус равен 6.