1. Разность двух углов, образовавшихся при пересечении двух прямых, равна 38°. Найдите все образовавшиеся неразвернутые углы. 2. Один из смежных углов в семь раз больше другого. Найдите углы, которые образует биссектриса большего угла со сторонами меньшего.
3. * Прямые АВ и CD пересекаются в точке О. ОК — биссектриса угла AOD, угол СОК = 127°. Найдите величину угла BOD.
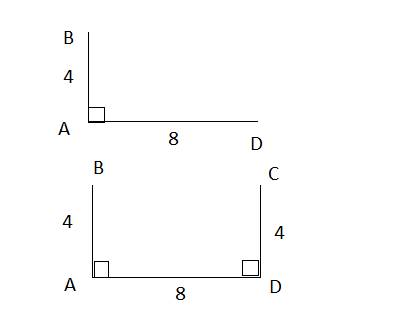

BD=CD по условию, а ED - общий катет. Отсюда ∠BDE=∠CDE,
а т.к. точки A,D,E лежат на одной прямой, то и ∠BDA=∠CDA.
(Заметим, что если Е совпала с D, то равенство углов ∠BDA и ∠CDA следует сразу из условия, т.к. BC⊥AD).
Далее, треугольники BDA и CDA равны по сторонам и углу между ними
(AD - общая, BD=CD по условию, ∠BDA=∠CDA доказали выше), а значит, AB=AC, что и требовалось.