30
Объяснение:
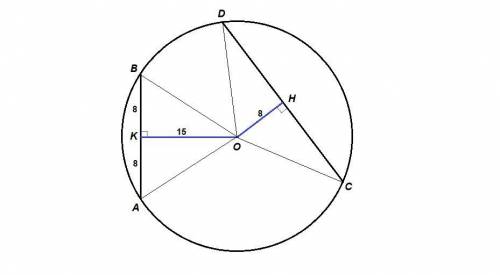
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и ОН⊥CD.
ОК = 15, ОН = 8 - расстояния от центра до хорд АВ и CD соответственно.
ΔАОВ равнобедренный, значит ОК - высота и медиана.
АК = КВ = 1/2АВ = 8
Из прямоугольного треугольника АОК по теореме Пифагора:
ОА = √(AK² + OK²) = √(8² + 15²) = √(64 + 225) = √289 = 17
ОС = ОА = 17
Из прямоугольного треугольника СОН по теореме Пифагора:
СН = √(CO² - OH²) = √(17² - 8²) = √(289 - 64) = √225 = 15
ΔOCD равнобедренный, значит ОН - высота и медиана.
CD = 2CH = 2 · 15 = 30
Дано :
Четырёхугольник ABCD — параллелограмм.
S(ABCD) = 36 см².
Точка О — точка пересечения диагоналей АС и BD.
ОН — расстояние от точки О до CD, OH = 3 см.
ОМ — расстояние от точки О до AD, AD = 2 см.
Найти :
Р(ABCD) = ?
Расстояние от точки пересечения диагоналей параллелограмма до стороны в два раза меньше соответствующий высоте (высоте, которая проведена к этой же стороне).
Следовательно —
Высота МF = 2*OM = 2*2 см = 4 см
Высота ЕН = 2*ОН = 2*3 см = 6 см.
Площадь параллелограмма равна произведению стороны и высоты, опущенной на эту сторону.
Отсюда —
S(ABCD) = MF*AD
36 см² = 4 см*AD
AD = 36 см²/4 см = 9 см
S(ABCD) = ЕН*CD
36 см² = 6 см*CD
CD = 36 см²/6 см = 6 см.
Периметр параллелограмма равен удвоенной сумме двух его смежных сторон.
Следовательно —
P(ABCD) = 2*(CD + AD) = 2*(6 см + 9 см) = 2*15 см = 30 см.
30 см.