1. Как называется линия, являющаяся графиком квадратичной функции? 1) прямая; 2) гипербола; 3) парабола; 4) окружность. 2. Какие из следующих функций являются квадратичными:
а) у = 3х2 – 2х + 1;
б)у = (х -3)2;
в) у = 5х – 1;
г) у = 9 – х2;
д) у = х3 + х2 + х;
е) у = - 0,6х.
3. Дана функция f(x) = x2 – 5x + a. Найти f(3), f (0), f(-3), f(-2,5).
4. Дана функция f(x) = -2,6х2 и указаны координаты точек
А(-3; 23,4); В(-5; -65); С(-2; -5,2); Д(4; 41,6).
Какие из этих точек не принадлежат графику данной функции?
5. Для каждой функции, заданной формулой, укажите координаты точки, в которой график функции пересекает ось у.
а) у = 2х2 – 4х -3;
б) у = х2 + 5х + 3;
в) у = -3х2 + х + 2.
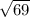это и будет медианой
1)так как диагонали ромба точкой пересечения деляться пополам, то(рассматривая маленький треугольник-четверть ромба) один катет=8(16:2), а другой катет=15(30:2). по теореме Пифагора:
8*8+15*15=гипотенуза*гипотенуза
289=гипотенуза в квадрате
гипотенуза(или сторона ромба)=17
2)проведем высоту из не острого угла ромба.
получим маленький прямоугольный треугольник(равнобедренный)
по теореме Пифагора:
2а квадрат=64
а квадрат=32
а=корень из 32
а=4корня из 2
а(высота!)
S=8*4корня из 2
3)так как мы знаем что в равнобедренном треугольнике высота являеться медианой, отрезки АН=СН=8см
по теореме Пифагора:
36+64=100
ВС=АВ=10см