в равнобедренном треугольнике высота будет также являться и медианой. а значит АМ=МС.
т.к. прямая BD перпендикулярна к отрезку АС, а также проходит через его середину, можно сказать, что ВD - серединный перепендикуляр, и по определению точки лежащие на серединном перпендикуляре равноудалены от его концов (Серединный перпендикуляр к отрезку – это множество точек, равноудаленных от концов отрезка.). а значит AD=CD, из этого следует, что треугольник ADC равнобедренный, что и требовалось доказать
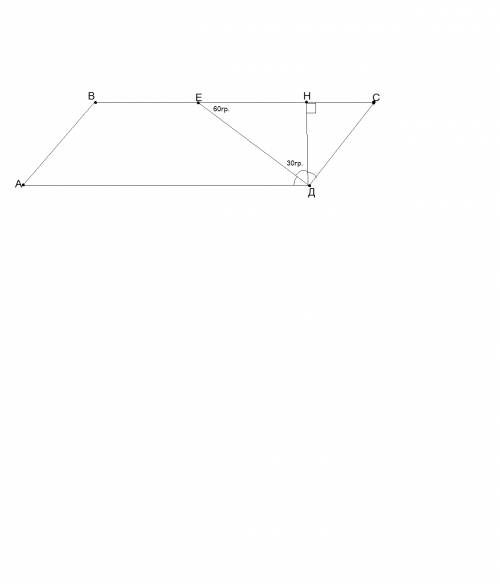
а). Проведем высоту ДН. Из треугольника ЕНД: угол НЕД=60гр., за условием задачи; угол ЕНД=90гр., так, как это угол при высоте; отсюда угол ЕДН=30гр.
Угол ВДА=НДА-ВДН. ВДН=30гр., АДН=90гр., как угол при высоте, отсюда угол ВДА=60гр.
Так, как ВД - бисектриса, то угол ВДА=ВДС=60гр. Отсюда угол АДС=120гр., отсюда угол ВСД=180гр.-АДС=180-120=60гр.
ответ: 120гр., 60гр.
б). Проведем высоту ДН. Из треугольника ЕНД: угол НЕД=60гр., за условием задачи; угол ЕНД=90гр., так, как это угол при высоте; отсюда угол ЕДН=30гр.
Угол ВДА=НДА-ВДН. ВДН=30гр., АДН=90гр., как угол при высоте, отсюда угол ВДА=60гр.
Так, как ВД - бисектриса, то угол ВДА=ВДС=60гр. Отсюда угол АДС=120гр., отсюда угол ВСД=180гр.-АДС=180-120=60гр.
Из треугольника ЕСД: угол СЕД=ДСЕ=60гр., отсюда можно зделать вывод, что этот треугольник равнобедренный, а значит ЕД=СД, и ДН будет медианой бисектрисой и высотой равнобедреного треугольника. Отсюда ЕН=НС=4/2=2см.
Из треугольника НСД: сторона НС лежит против угла 30гр., у прямоугольном треугольнике, отсюда можно узнать ее гипотенузу: 2*2=4см. Сторона ВС=ВЕ+ЕС=3+4=7см. Отсюда сторона СД=4см. Отсюда периметр треугольника равен (4+7)*2=22см.
ответ:22см.
в). Четереугольник АВЕД будет равнобедренной трапецыей так, как сторона ВЕ паралельна стороне АД, и при основании угли равные ( угол АВЕ=120гр.; ВЕД=120грю; ВАД=60гр.; ЕДА=60гр.
Разьяснила, как можно по доходчевей))) Поставь лучшее решение мне, тебе несколько пунктов вернеться, и мне несколько начислиться))) Если что то не понятно, обращайся))
160°
Объяснение:
1) Прямой угол 90° разбит на 2 угла: х и 8х.
Находим х:
х+8х=90
9х = 90
х=10°.
2) Диагонали прямоугольника разбивают его на 2 пары равнобедренных треугольников, общая вершина которых лежит в точке пересечения диагоналей.
3) В равнобедренном треугольнике, у которого угол при вершине тупой, в основании лежат 2 равных между собой острых угла, каждых их которых равен 10°.
4) Т.к. сумма внутренних углов треугольника равна 180°, то тупой угол, образованный пересечением диагоналей, равен:
180 - 10*2 = 180 - 20 = 160°.
ответ: 160°.