См. вложение.
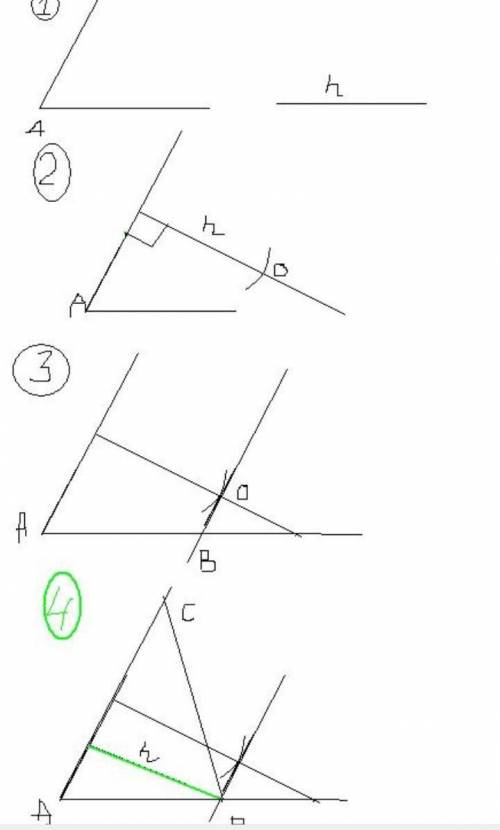
1 дано угол и выстоа
2 Обозначим вершину данного угла буквой А. Строишь перпендикуляр к стороне в любом месте. На перпендикуляре откладываешь высоту. Получилась точка О.
3 Через нее, через точку О то есть, строишь еще один перпендикуляр, чтоб получилась линия параллельная боковой стороне. На ее пересечении с основанием находишь точку В.
4 В точке В строишь заданный угол, только в другую сторону и на пересечении линий находишь точку С. Три точки есть, треугольник построен. Можно проверить длину полученной высоты, показанна зелённым.
Даны три отрезка: АС - основание треугольника, ВС - одна из его сторон, ВН - высота треугольника. Нужно построить треугольник АВС.
Построение.
Проведем две полуокружности равного радиуса с центрами на произвольной прямой а так, чтобы они пересеклись по обе её стороны. Через точки пересечения проведем прямую. Она перпендикулярна первой ( такой построения перпендикуляра к прямой является стандартным).
Отметим точку пересечения построенной прямой с прямой а буквой Н. Эта точка – основание высоты. От Н отложим отрезок НВ длиной, равной длине заданной высоты.
Из В как из центра радиусом, равным длине заданной стороны ВС, проведем полуокружность до пересечения с прямой а. Отметим т.С - вторую вершину искомого треугольника.
От т.С отложим отрезок СА, равный длине основания.
Соединим точки А, В, С. Искомый треугольник АВС построен.

12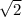
Объяснение: