Приведите примеры векторных величин, известных вам из курса физики.
Ускорение (а), скорость (V), ускорение свободного падения (g).
Дайте определения вектора. Объясните, какой вектор называется нулевым.
Вектор - это отрезок имеющий направление. Вектор называется нулевым, если его начало совпадает с его концом, (т.е. длина 0)
Что называется длиной ненулевого вектора? Чему равна длина нулевого вектора?
Длина ненулевого вектора не равна 0, и его начало не совпадает с его концом. Длина нулевого вектора равна 0.
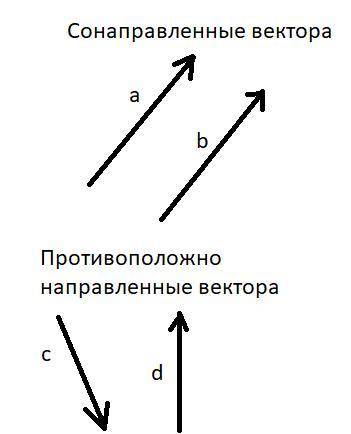
Какие вектора называются коллиниарными? Изобразите на рисунке сонаправленные вектора a и b и противоположно направленные вектора c и d.
Вектора коллинеарны, если они параллельны, (или лежат на одной плоскости).
Дайте определения равных векторов.
Вектора равны, если они сонаправлены и их длины равны.
Только так, не забудь на рисунке вектора над буквами подписать
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. Данный треугольник Пифагоров и гипотенуза равна 5см.
Точка М - центр описанной окружности.
Точка О - центр вписанной окружности.
Тогда R=2,5см, то есть ВМ=2,5см.
Радиус вписанной окружности равен по формуле:
r=(AC+BC-АВ)/2 = 2/2=1см.
Итак, СН=r=1см => HB=3-1=2см.
PB=HB=2см (касательные из одной точки).
Тогда МР=2,5-2=0,5см. В прямоугольном треугольнике ОМР по Пифагору:
ОМ=√(1²+0,5²)= √1,25 ≈ 1,118 ≈ 1,12см .
ответ: расстояние между центрами окружностей равно
√1,25 ≈ 1,12 см.
Или так: по теореме Эйлера в треугольнике расстояние между центрами вписанной и описанной окружностей находится по формуле:
d² = R² - 2·R·r.
В нашем случае R = 2,5см, а r = 1cм.
тогда d = √(2,5² -2·2,5) = √(2,5·0,5) = √1,25 ≈ 1,12 см.

тоесть нам нужно доказать что длина АВ равна 8
АВ=8, что и требовалось доказать