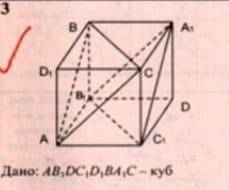
Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.
--------------
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
---------------
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.

A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
-----------
теперь по теореме пифагора найдем AH:
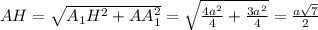
ответ: 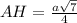
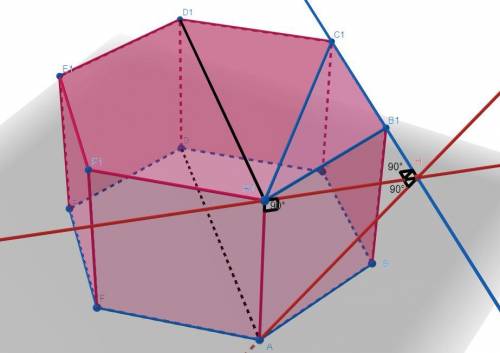
а) У ромба все стороны равны из этого следует что P=a*4; 32см :4=8см
ответ: стороны ромба 8см
б) 2( x + 2x) = 24 ; 6x = 24 ; x = 4 ; a = 4одна сторона; b = 8 другая сторона.
в) Средняя линия треугольника равна половине соответствующей стороны, значит сторона равна 14см.
г) Пусть одна сторона будет х, а другая х+5, тогда: 2·(х+х+5)=50
2·(2х+5)=50 ; 4х+10=50 ; 4х=50-10 ; 4х=40 ; х=40:4 ; х=10
Значит одна сторона х=10 см, а другая х+5=10+5=15 см.
д) Делим ромб диагоналями на 4 равных прямоугольных треугольника.Т.к диагонали делят углы ромба пополам то в этих треугольничках один из углов 60:2=30*.Катет лежащий против угла в 30 градусов равен половине гепотенузы (16:4=4) => половина меньшей диагонали 4:2=2 => вся меньшая диагональ 2*2=4 см.
e) Средняя линии трапеции равна сумме длин двух оснований=> 10+22/2=32/2=16 см
ж) В прямоугольнике диагонали равны 18:2=9. ответ: Диагонали по 9 см.
и) Периметр 1*4=4 см; Площадь 1*1=1 см2
к) У квадрата 4 стороны. По свойству квадрата они равны между собой, поэтому: 64/4= 16 см - каждая сторона площадь квадрата равна произведению двух его сторон, поэтому площадь квадрата = 16*16=256 см2