Вектор EF имеет координаты (2-(-2); 2-0) = (4; 2). Его длина Вектор FM имеет координаты (4-2; -2-2) = (2; -4). Его длина Вектор MN имеет координаты (0-4; -4-(-2)) = (-4; -2). Его длина Вектор NE имеет кооординаты (-2-0; 0-(-4)) = (-2; 4). Его длина Все стороны четырёхугольника равны. Найдём углы между ними: Все стороны равны, угол между сторонами прямой. Значит, EFMN - квадрат.
1. Катет лежащий напротив угла в 30*= половине гипотенузы, в данном случае 8. Второй катет находится по т. Пифагора и =8 корней из 3 2. Пускай первый катет=x, тогда второй= x-10, а гипотенуза х+10. По теореме Пифагора получается два корня 0 и 40. 0 не подходит, тогда выходит, что первый катет = 40, второй 30, а гипотенуза 50. Периметр = 120см. Площадь прямоугольного треугольника = половине произведения катетов, то есть 60см квадратных. 3. Если треугольник равнобедренный, то по формуле площади S=1/2ah, где а -боковая сторона, h - высота, получается, что 48=1/2•а•8, отсюда а=12.
Тр-к АВС-прямоугольный(уголС=90) Из точки С проводим перпундикуляр на плоскость (СК), точку к соединяем с А и В, тогда Ак, Ск-проекции катетов данного тр-ка! ПустьАС=ВС=а СК=1/2 *АС; (катет, лежащий против угла в 30град) СК=1/2 *а=а/2 В тр-ке АВС проводим СМ перпенд-но АВ(через середину АВ!), уголСМК-это угол между плоскостью (АВС) и альфа Из СКМ(угол СКМ=90град): СК/СМ=sinx Из тр-каАСМ: СМ=АМ(уг.А=угВ=45град; уг.АСМ=90-45=45 sin45=CM/AC; CM=(a coren2)/2 sinx=(a/2):(acoren2)/2 =1/coren2; x=45 ; 45град
Вектор EF имеет координаты (2-(-2); 2-0) = (4; 2). Его длина
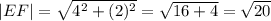
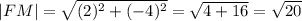
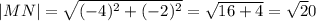
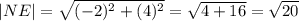
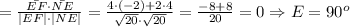
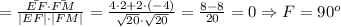
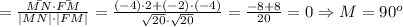
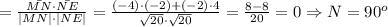
Вектор FM имеет координаты (4-2; -2-2) = (2; -4). Его длина
Вектор MN имеет координаты (0-4; -4-(-2)) = (-4; -2). Его длина
Вектор NE имеет кооординаты (-2-0; 0-(-4)) = (-2; 4). Его длина
Все стороны четырёхугольника равны. Найдём углы между ними:
Все стороны равны, угол между сторонами прямой. Значит, EFMN - квадрат.