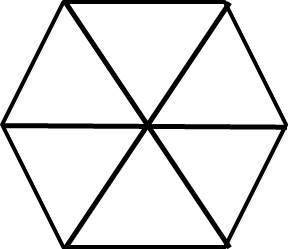
Сторона правильного шестиугольника равна радиусу описанной окружности, т.е. а = R.
Т.к. проведя все радиусы в шестиугольнике, вписанном в окружность, мы разобьем его на 6 равносторонних треугольников (см. рис.), а площадь получившегося треугольника можно найти по формуле
1/2 · R · R · sin60° = 1/2 · R² · √3/2 = R²√3/4
(полный круг составляет 360°, тогда угол при вершине равностороннего треугольника будет равен 60°, а sin60° = √3/2), то площадь шестиугольника будет равна:
6 · R²√3/4 = 3R²√3/2 = 3 · 2²√3/2 = 6√3 (см²)
ответ: 6√3 см².
Если известны величины двух углов произвольного треугольника (β и γ), то величину третьего (α) можно определить исходя из теоремы о сумме углов в треугольнике. Она гласит, что эта сумма в евклидовой геометрии всегда равна 180°. То есть для нахождения единственного неизвестного угла в вершинах треугольника отнимайте от 180° величины двух известных углов: α=180°-β-γ.2Если речь идет о прямоугольном треугольнике, то для нахождения величины неизвестного острого угла (α) достаточно знать величину другого острого угла (β). Так как в таком треугольнике угол, лежащий напротив гипотенузы, всегда равен 90°, то для нахождения величины неизвестного угла отнимайте от 90° величину известного угла: α=90°-β