
y=3·x+4
Объяснение:
Абсцисса координат точек M(-2;-2) и N(2;10) различные (то есть прямая не проходит вертикально) и поэтому будем искать уравнение прямой в виде с угловым коэффициентом:
y=k·x+b.
Так как прямая проходить через точки M(-2;-2) и N(2;10), то подставим координаты точек в уравнение и получим систему уравнений относительно k и b:
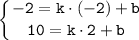
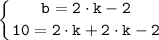
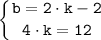
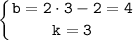
Подставляем найденные решения получим:
y=3·x+4.
Для решения задачи можно использовать общий вид уравнения прямой, проходящей через 2 точки M(x₁; y₁) и N(x₂; y₂):
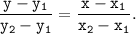
При заданных значениях координат M(-2;-2) и N(2;10) имеем:
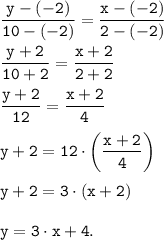
По свойству медиан : медианы пересекаются и точкой пересечения делятся в отношении2/1 считая от вершины.Значит ВМ это часть медианы и составляет 2 части.
Проведем медиану на сторону АС . Она будет состоять из трех частей и ВМ принадлежит медиане . одна часть медианы равна 3( 6/2). Значит вся медиана на сторону АС равна 3*3=9 и она будет являться высотой так как треугольник АВС равнобедренный АВ=ВС. И по формуле найдём площадь треугольника АВС S= 9(Высота)*10(сторона , к которой проведена высота)/2=45
ответ:45
30,40,110 градусов
Пусть А и С Основания перпендикуляров опущенных из точки М на стороны данного угла с вершиной О,Точка В Основание перепендикуляра опущенного из точки М на луч,проходящий между сторонами угла АОС причём АОВ = 30градус и СОВ =40градус.Из точек А В С отрезок ОМ виден под прямым углом значит эти точки лежат на окружности с диаметром ОМ Вписанные в эту окружность углы АСВ и АОВ опираются на одну и ту же дугу поэтому АСВ = АОВ = 30градус.Анологично ВАС=СОВ =40градус Следовательно АВС = 180градус - 30градус - 40=110