12√1326 cм²
Объяснение: Применяем метод удвоения медианы.
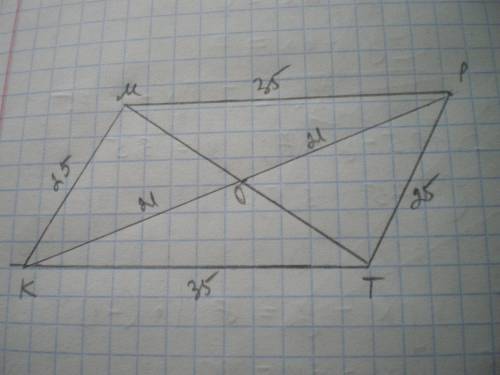
Дан ΔКМТ, КМ=25 см, КТ=35 см, КО - медиана, КО=21 см. Найти S(КМТ).
На продолжении медианы КО за точку О отложим отрезок, равный КО.
Рассмотрим четырёхугольник КМРТ.
КM=РТ; РM=ТК
(Диагонали четырёхугольника делятся точкой пересечения О пополам). Четырёхугольник КМРТ – параллелограмм.
Рассмотрим ΔКМР. КМ=25 см, МР=35 см, КР=42 см.
По формуле Герона S(КМР)=√(р(р-а)(р-b)(p-c))=√(51*26*16*9)=12√1326 cм.²
S(КМРТ)=2SКМР=24√1326 cм²;
S(КМТ)=1/2 S(КМРТ)=12√1326 cм²;
В прямоугольном треугольнике катет, лежащий против угла в 30 градусов, равен половине гипотенузы. Значит, катет равен 18:2 = 9.
Если один острый угол прямоугольного треугольника равен 45, то второй тоже равен 45, т.к. сумма острых углов в прямоугольном треугольнике равна 90 градусов.
Треугольник равнобедренный. Если один катет равен 8, то и второй равен 8.
Если сумма катетов 28 и они равны, то каждый катет равен 28:2 = 14.
В прямоугольном равнобедренном треугольнике медиана вершины угла равна биссектрисе и высоте. А медиана из прямого угла в прямоугольном треугольнике равна половине гипотенузы.
Значит х+2х=21. Отсюда х=7 2х=14.
Гипотенуза равна 14, высота равна 7.